Các câu hỏi tương tự
Cho bảng tần số, tần suất ghép lớp như sau:
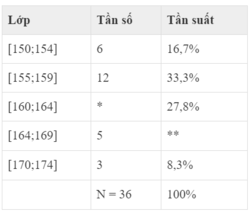
a) Giá trị * là:
A. 8 B. 10
C. 12 D. 13
b) Giá trị ** là:
A. 3,9% B. 5,9%
C. 13,9% D. 23,9%
Cho đường tròn (C) có phương trình
x
2
+
y
2
−
6
x
+
4
y
−
12
0
và điểm A(m; 3). Giá trị của m để từ A kẻ được hai tiếp tuyến vuông góc đến (C) là A. m 2 hoặc m 8 B.m - 2 hoặc m - 8 C.m 2 hoặc m - 8 D.m - 2 hoặc m 8
Đọc tiếp
Cho đường tròn (C) có phương trình x 2 + y 2 − 6 x + 4 y − 12 = 0 và điểm A(m; 3). Giá trị của m để từ A kẻ được hai tiếp tuyến vuông góc đến (C) là
A. m = 2 hoặc m = 8
B.m = - 2 hoặc m = - 8
C.m = 2 hoặc m = - 8
D.m = - 2 hoặc m = 8
Tìm các giá trị của tham số m để phương trình
m
x
2
+
2
(
2
m
-
1
)
x
+
m
+
2
0
vô nghiệm A.
3
-
6
3
m...
Đọc tiếp
Tìm các giá trị của tham số m để phương trình m x 2 + 2 ( 2 m - 1 ) x + m + 2 = 0 vô nghiệm
A. 3 - 6 3 < m < 3 + 6 3
B. Không tồn tại m
C. m < 1/12
D. m ≠ 0; m < 1/12
Hệ phương trình sau vô nghiệm khi tham số m nhận giá trị:
![]()
A. m = 4 B. m = -3
C. m = 2 D. m = -12
Giá trị của a mà
[
a
;
a
+
1
2
]
⊂
(
−
∞
;
−
1
)
∪
(
1
;
+
∞
)
là A. a
≤
-3 B. a 1 C. a -3 D. a -3 hoặc a
≥...
Đọc tiếp
Giá trị của a mà [ a ; a + 1 2 ] ⊂ ( − ∞ ; − 1 ) ∪ ( 1 ; + ∞ ) là
A. a ≤ -3
B. a > 1
C. a < -3
D. a < -3 hoặc a ≥ 1
Cho π/2 < a < 3π/4. Giá trị tan2a là
A. -2 7 B. 3 3 /4
C. -3 7 D. 3 7
Câu 1.
a) Cho tập A,B lần lượt là tập xác định của hàm số f(x) = \(\sqrt{6-x}\) và g(x) = \(\dfrac{3}{2x+1}\). Xác định các tập A∩B, A∪B, A∖B, CRA.
b) Cho tập hợp C=[−3;8] và D=[m−6;m+3). Với giá trị nào của m thì C∩D là một đoạn thẳng có độ dài bằng 4.
Câu 2. (1,0 điểm).
a/ Cho hai tập hợp A = {1;3;5;8}, B={3;5;7;9). Xác định tập hợp AUB; AVB
b/ Tìm a nguyên thuộc [-2023; 2023] Cho biết [3;12)\(-∞;a) = 0.
Cho các số thực dương x,y thỏa mãn x+2y+3xy=3 . Biết rằng biểu thức P= x+y đạt giá trị nhỏ nhất bằng \(\frac{a\sqrt{b}-c}{3}\)
trong đó a,b,c là các số nguyên dương . Gọi S là tập hợp các giá trị của M= a+b+c , tính tổng bình phương các phần tử của S







