Đáp án B.
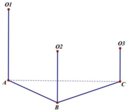
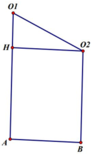
Gọi O1, O2, O3 lần lượt là tâm của 3 mặt cầu và A, B, C lần lượt là hình chiếu của 3 tâm trên mặt phẳng đã cho.

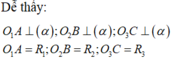

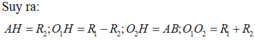
![]()
![]()
![]()
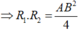
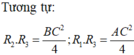
![]()
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Đáp án B.
Gọi O1, O2, O3 lần lượt là tâm của 3 mặt cầu và A, B, C lần lượt là hình chiếu của 3 tâm trên mặt phẳng đã cho.



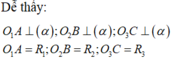


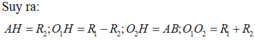
![]()
![]()
![]()
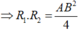
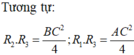
![]()
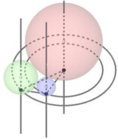
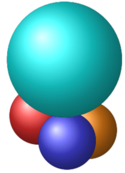
Ba quả bóng dạng hình cầu có bán kính bằng 1 đôi một tiếp xúc nhau và cùng tiếp xúc với mặt phẳng (P). Mặt cầu (S) bán kính bằng 2 tiếp xúc với ba quả bóng trên. Gọi M là điểm bất kì trên (S), MH là khoảng cách từ M đến mặt phẳng (P). Giá trị lớn nhất của MH là
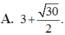
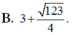
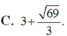
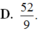
Xét tám mặt cầu có bán kính bằng 1 và các mặt cầu này đều tiếp xúc với cả ba mặt phẳng tọa độ. Tìm bán kính mặt cầu (S) mà cả tám mặt cầu kể trên đều tiếp xúc trong với (S)
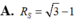
![]()
![]()
![]()
Trong Oxyz xét các mặt cầu bán kính bằng 1 và đều tiếp xúc với cả 3 mặt phẳng tọa độ. Gọi (S) là mặt cầu tiếp xúc trong với tất cả các mặt cầu trên. Tính bán kính R của (S).
![]()
![]()
![]()
![]()
Trong không gian cho bốn mặt cầu có bán kính lần lượt là 2; 3; 3; 2 (đơn vị độ dài) đôi một tiếp xúc nhau. Mặt cầu nhỏ tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng
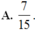
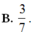
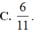
![]()
Trong không gian Oxyz, cho các điểm A, B, C (không trùng O) lần lượt thay đổi trên các trục Ox, Oy, Oz và luôn thỏa mãn điều kiện: tỉ số giữa diện tích của tam giác ABC và thể tích khối tứ diện OABC bằng 3/2. Biết rằng mặt phẳng (ABC) luôn tiếp xúc với một mặt cầu cố định, bán kính của mặt cầu đó bằng:
A. 3.
B. 2.
C. 4.
D. 1.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;2;1), B(3;-1;1), C(-1;-1;1). Gọi S 1 là mặt cầu tâm A, bán kính bằng 2; S 2 và S 3 là hai mặt cầu có tâm lần lượt là B, C và bán kính đều bằng 1. Trong các mặt phẳng tiếp xúc với cả 3 mặt cầu S 1 , S 2 , S 3 có bao nhiêu mặt phẳng vuông góc với mặt phẳng (Oyz)?
A. 3
B. 1
C. 4
D. 2
Một khối đa diện được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ.
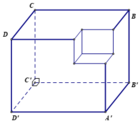
Gọi S là khối cầu có thể tích lớn nhất chứa trong H và tiếp xúc với các mặt phẳng (A'B'C'D'), (BCC'B') và (DCC'D'). Tính bán kính của S.
A . 2 + 3 3
B . 3 - 3
C . 2 3 3
D . 2
Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là a và 2a sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Tính bán kính đáy r của hình nón đã cho.
A. r = 8 a 3
B. r = 2 2 a
C. r = 4 a 3
D. r = 2 a
Trong không gian Oxyz, cho các điểm A, B, C (không trùng O) lần lượt thay đổi trên các trục Ox, Oy, Oz và luôn thỏa mãn điều kiện : tỉ số giữa diện tích của tam giác ABC và thể tích khối OABC bằng 3 2 . Biết rằng mặt phẳng (ABC) luôn tiếp xúc với một mặt cầu cố định, bán kính của mặt cầu đó bằng :
A. 3
B. 2
C. 4
D. 1