Ta có thể xác định hai điểm M thỏa mãn như dưới hình.
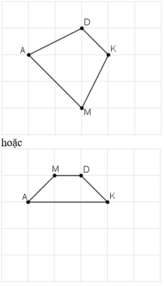
Ta có thể xác định hai điểm M thỏa mãn như dưới hình.

Cho ba điểm A, B, C trên giấy kẻ ô vuông ở hình bên. Hãy vẽ điểm thứ tư M sao cho A, B,C, M là 4 đỉnh của một hình bình hành.

Cho hình thang cân ABCD có O là giao điểm của 2 đường chéo, H là trung điểm của đáy nhỏ AB. Từ B kẻ đường thẳng BE//AD, từ A kẻ À//BC (E, F đều thuộc DC).Gọi I là giao điểm của AE và BF. Qua I kẻ đường thẳng IK⊥DC tại K. CMR:
a)Tứ giác ABEF là hình thang cân
b) Bốn điểm H, O, I, K cùng nằm trên 1 đường thẳng
Cho hình chữ nhật ABCD. O là giao điểm hai đường chéo và một điểm P bất kì trên đường chéo BD (P nằm giữa O và D). Gọi M là điểm đối xứng của C qua P. a) Chứng minh tứ giác AMDB là hình thang. Xác định vị trí của P trên BD để AMDB là hình thang cân. b) Kẻ ME vuông góc AD, MF vuông góc BA. Chứng minh EF // AC và 3 điểm E, F, P thẳng hàng. c) Xác định vị trí P trên BD để tứ giác nối 4 điểm A, M, D, B là hình thang cân. d) Nếu hình chữ nhật ABCD có AB = 2BC. Gọi K là điểm trên AB sao cho góc ADK = $15^o$. Chứng minh tam giác CDK cân.
Cho hình thang cân ABCD (AB song song CD), (AB<CD).Từ A kẻ AH vuông góc với AB cắt AB tại H. Từ B kẻ BK vuông góc với AB cắt AC tại K.
a) Tứ giác AHKB là hình gì? Vì sao?
b) Gọi E là trung điểm của Ab, F là trung điểm của DC, I và G theo thứ tự là giao điểm của AC với BD và CH với DK. Chứng minh rằng bốn điểm E, I, G, H thẳng hàng.
cho tam giác abc vuông tại a tia phân giác của góc b cát ac tại d trên tia bc lấy điểm e sao cho ba=be kẻ ah vuông góc với bc tại h
a)CM:△abd=△akd
b)gọi ba,ed giao nhau tại k cmr: tứ giác aeck là hình thang cân
c)gọi bd và ah giao nhau tại m tứ giác meca là hình gì vì sao
giúp mình với mk cần gấp
Cho hình thang cân ABCD ( AB//CD , AB < DC ) . Kẻ AH vuông góc vs AB cắt DB tại h . Kẻ BK vuông góc với AB và cắt AC tại K
a) Tứ giác AHKB là hình gì . tại sao
b) gọi E là trung điểm cua AB , F là trung điểm của DC . gọi i là giao diểm của AC và BD , g là giao điểm của ch và dk . cm : ei , g , f thẳng hàng
cho tg ABC cân tại A. Từ điểm D trên BC kẻ đường vuông góc với BC cắt AB, Ac lần lượt tại E, F. Dựng các hình chữ nhật BDEH và CDFK
a) CM: Ba điểm A, H, K thẳng hàng
b) CM: A là trung điểm của HK
c) Gọi I, J theo thứ tự là tâm của các hình chữ nhật BDEH và CDFK. Tìm tập hợp trung điểm M của IJ khi D di động trên BC
Tứ giác ABCD là hình thang cân, có O là giao 2 đường chéo. H là trung điểm đáy nhỏ AB. Từ B kẻ BE //AD. Từ A kẻ AF//BC(E,F thuộc DC). Gọi I là giao của AE và BF qua I kẻ IK vuông góc DC tại K. CMR:a, ABEF là hình thang cân b,4 điểm H,D,I,K cùng nằm trên 1 đường thẳng.
Cho hình thang cân ABCD, O là giao điểm hai đường chéo, H là trung điểm đáy AB. Kẻ BE // AD, kẻ AF // BC ( E,F thuộc BC ). I là giao điểm của AE, BF. Qua I, kẻ IK vuông góc với DC tại K.
a ) Chứng minh : ABEF là hình thang cân
b ) H, O, I, K thẳng hàng