Các câu hỏi tương tự
Cho ba biểu thức M
(
x
+
y
)
2
; N
x
x
-
y
y
x
-
y
; P
x
-...
Đọc tiếp
Cho ba biểu thức M = ( x + y ) 2 ; N = x x - y y x - y ; P = x - y ( x + y ) . Biểu thức nào bằng với biểu thức x + xy + y với x, y, x ≠ y không âm?
A. M
B, N
C. P
D. M.N
1. Cho x,y,z là ba số dương thay đổi và thỏa mãn ^{x^2+y^2+z^2le xyz}Hãy tìm giá trị lớn nhất của biểu thức Afrac{x}{x^2+yz}+frac{y}{y^2+zx}+frac{z}{z^2+xy}2. Cho x,y,z là các số thực không âm thỏa mãn x^2+y^2+z^23Tìm giá trị lớn nhất của biểu thức Bxy+yz+zx+frac{5}{x+y+z}
Đọc tiếp
1. Cho x,y,z là ba số dương thay đổi và thỏa mãn \(^{x^2+y^2+z^2\le xyz}\)
Hãy tìm giá trị lớn nhất của biểu thức \(A=\frac{x}{x^2+yz}+\frac{y}{y^2+zx}+\frac{z}{z^2+xy}\)
2. Cho x,y,z là các số thực không âm thỏa mãn \(x^2+y^2+z^2=3\)
Tìm giá trị lớn nhất của biểu thức \(B=xy+yz+zx+\frac{5}{x+y+z}\)
Tìm GTNN của biểu thức biết x,y không âm và \(x+y=2\):
a) \(P=\sqrt{x}+\sqrt{y}\)
b)\(Q=\sqrt[3]{x}+\sqrt[3]{y}\)
c)\(S=\sqrt[n]{x}+\sqrt[n]{y}\)
Cho biểu thức A=\(\frac{\left(\sqrt{x}+\sqrt{y}\right)^2}{x\sqrt{x}+y\sqrt{y}}\left(\frac{x-y}{\sqrt{x}-\sqrt{y}}-\frac{x\sqrt{x}-y\sqrt{y}}{x-y}\right)\)
a Rút gọn biểu thức A
b so sánh A và \(\sqrt{A}\)
\(\text{Các số thực không âm x,y,z thay đổi thỏa mãn điều kiện: x^2+ y^2+x^2+x^2y^2+y^2z^2+z^2x^2=6. \text{Tìm giá trị lớn nhất và nhỏ nhất của biểu thức Q=x+y+z}}\)\(\text{Các số thực không âm x,y,z thay đổi thỏa mãn điều kiện x^2+y^2+z^2+x^2y^2+y^2z^2+z^2x^2=6. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức Q=x+y+z}\)
Cho các số dương \(x,y\varepsilon R\)thỏa mãn \(\sqrt{xy\left(x-y\right)}=x+y\). Tìm giá trị nhỏ nhất của biểu thức P=x+y
Với các số không âm x,y,z thỏa \(x^2+y^2+z^2=2\)
a, Chứng mình: x + y +z >= 2 + xy
b. Tìm GTLN của biểu thức \(P=\frac{x}{2+yz}+\frac{y}{2+xz}+\frac{z}{2+xy}\)
Tìm GTNN của biểu thức \(P=x^3+y^3+xy\), biết x,y thuộc R và x+y=1
21 Cho ba số phân biệt a,b,c . Chứng minh rằng biểu thức
A=a^4(b-c)+b^4(c-a)+c^4(a-b) luôn khác 0
23 Cho x, y là các số dương thỏa mãn điều kiện 9y(y-x)= 4x^2
Tính giá trị biểu thức\(\frac{x-y}{x+y}\)
24 Cho x,y là số khác 0 sao cho 3x^2-y^2=2xy
Tính giá trị của phân thức A= \(\frac{2xy}{-6x^2+xy+y^2}\)




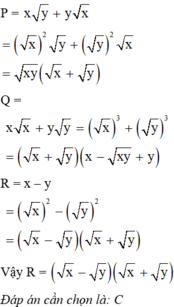

![Yuri Sweet[𝕿𝖊𝖆𝖒 𝕹𝖊𝖕𝖆𝖑]](https://hoc24.vn/images/avt/avt6428199_256by256.jpg)





