a: \(B\left(x\right)-A\left(x\right)=-3x+9-x^3+3x^2-7x+5\)
\(=-x^3+3x^2-10x+14\)
b: B(x)=-3x+9
Bậc là 1
Đặt B(x)=0
=>-3x+9=0
=>-3x=-9
hay x=3
c: B(3/5)=-9/5+9=7,2
Cho hai đa thức
P(x) =5x4 +x - 2x2 - 5
Q(x) =7 - 3x -4x2 +5x4
a.) sắp xếp các đa thức trên theo lũy thừa giảm dần của biến.
b.) Tính P(x) + Q(x) và P(x) - Q(x)
Tam giác ABC có BC=a, AC=b và ha, hb là độ dài các đường cao tương ứng. Xác định dạng của tam giác biết rằng:
a) ha = hb
b) a = hb
c) a=ha, b=hb
cho tam giác abc vuông tại a có bc=2ab. tia phân giác góc b cắt ac tại .a, chứng minh bd=cd b, tính góc b và góc c của tam giác abc
Cho tam giác ABC có AB=AC=5cm BC=6cm đường cao AH xuất phát từ đỉnh A của tam giác ABC (H thuộc BC) a)chứng minh tam giác AHB =AHC b)chứng minh AH là tia phân giác của góc A c)tính độ dài các đoạn thẳng BH và AH
Cho tam giác ABC. Hai đường phân giác của các cặp góc ngoài đỉnh B và C, đỉnh C và A, đỉnh A và B lần lượt cắt nhau tại A', B', C'. Chứng minh rằng AA', BB', CC' là các đường cao của tam giác A'B'C'. Từ đó suy ra giao điểm của ba đường phân giác của tam giác ABC là trực tâm của tam giác A'B'C' ?
Cho tam giác ABC có hai đường cao AD và BE cắt nhau tại M. Tính số đo góc AMB biết góc A=55o góc B=67o
Cho tam giác ABC hạ đường cao từ đỉnh A và B xuống các cạnh đối diện không nhỏ hơn các cạnh ấy. Tính các góc trong tam giác ABC
Cho góc xOy=60 độ. Trên tia Ox lấy điểm A, qua A kẻ đường thẳng vuông góc với Oy tại D. Trên tia đối của tia DO lấy điểm B, qua B kẻ đường thẳng vuông góc với Ox tại E, BE cắt AD tại I.
a) CM: OI⊥AB
b) Tính góc AIB
Giúp mình giải với ạ
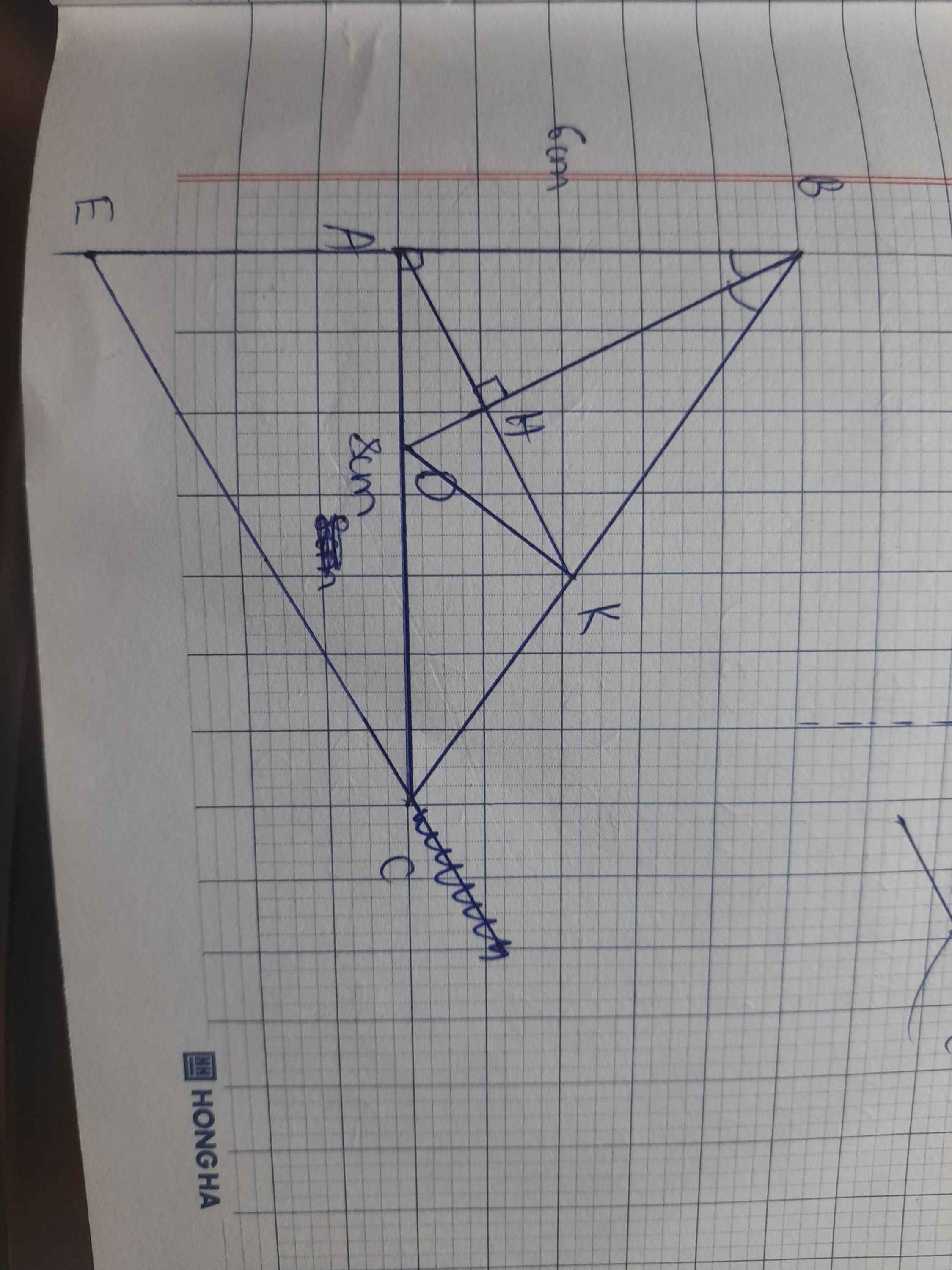
Cho ∆abc vuông tại a có ab=6cm, ac=8cm. Tia phân giác của góc abc cắt ac tại d.
a)Tính bc
b) Kẻ ah vuông góc với bc, tia ah cắt bc tại k. Chứng minh:∆ahb=∆khb
c) Chứng minh:dk vuông góc với bc
d) Qua c kẻ đường thẳng song song với ak, cắt tia ba tại e. Chứng minh:2(ad+ae)>ec
