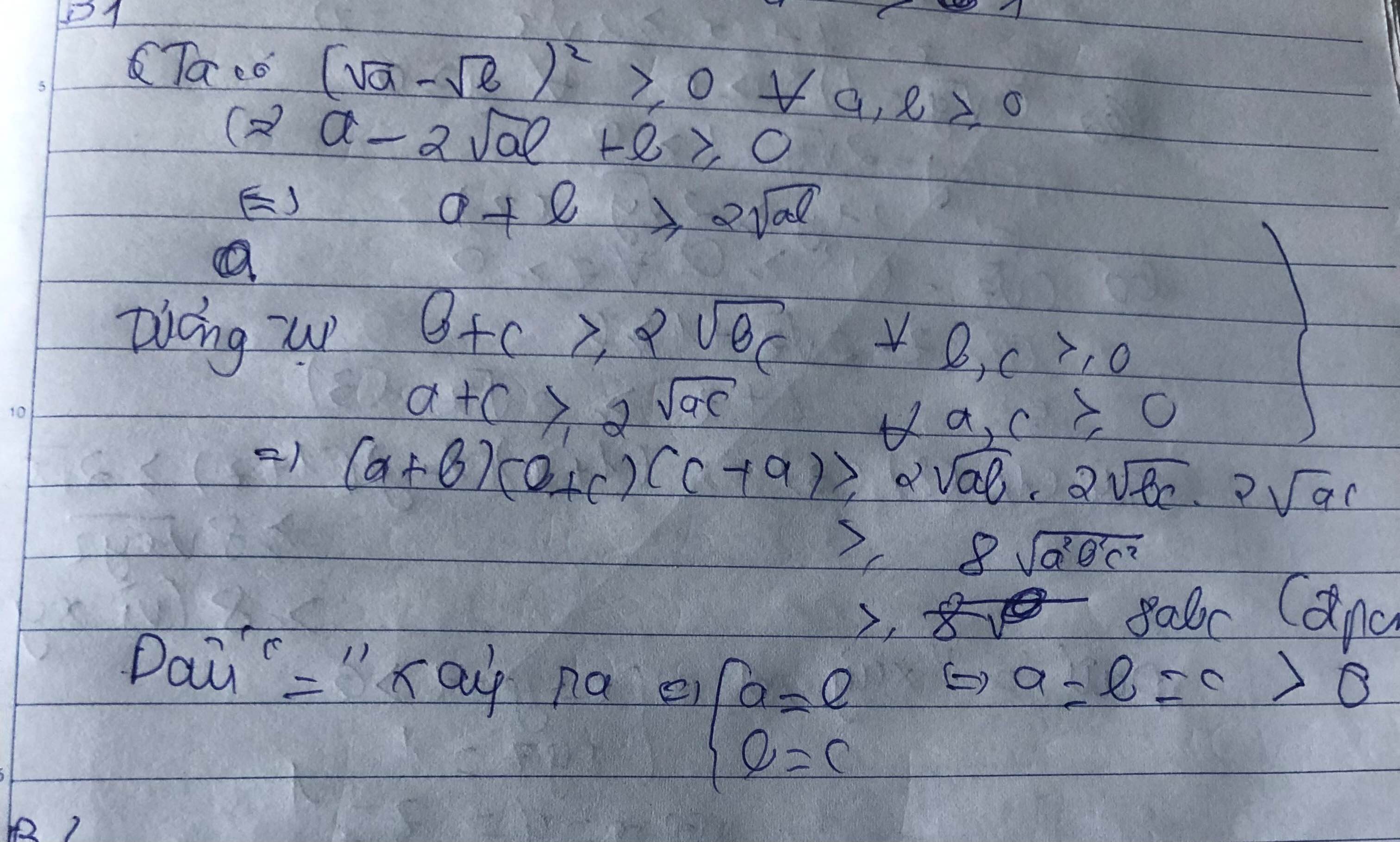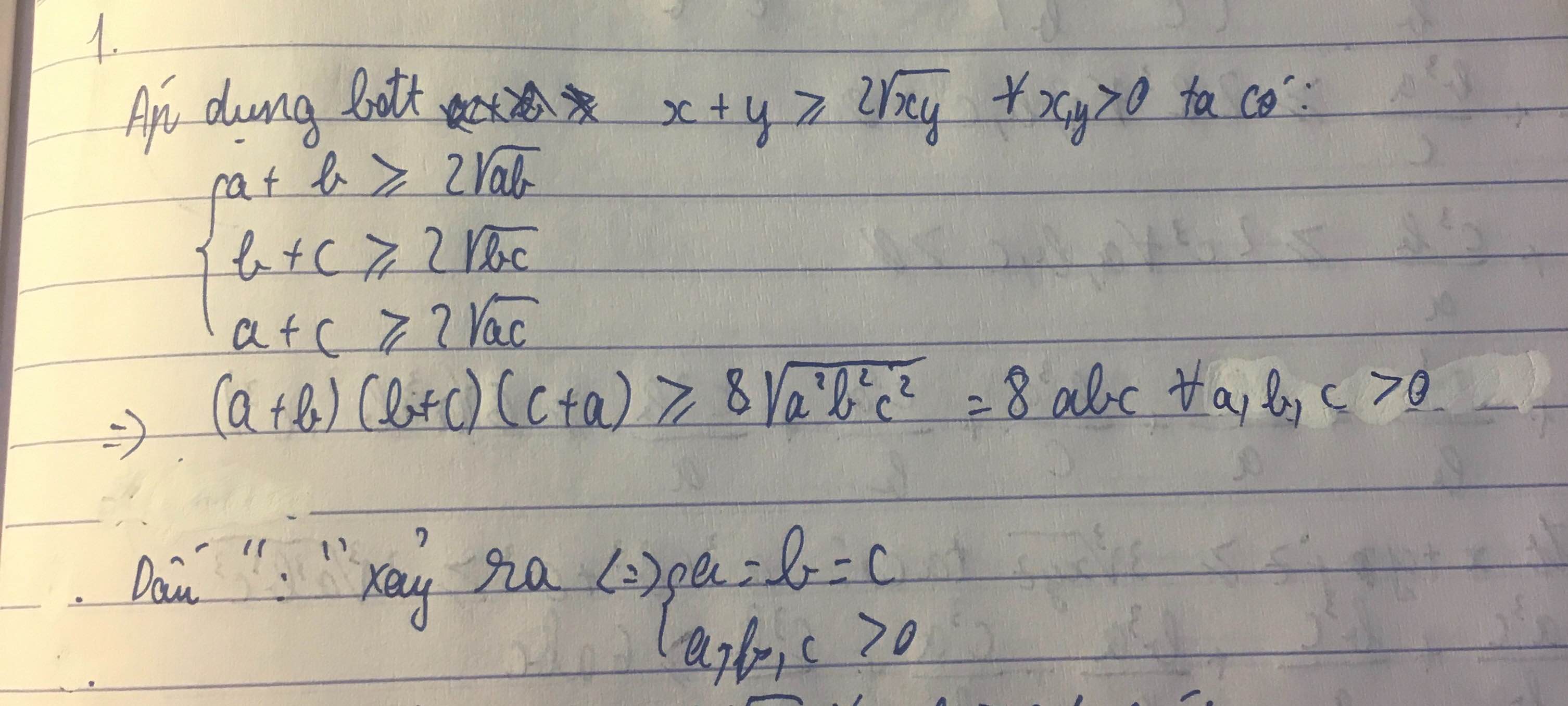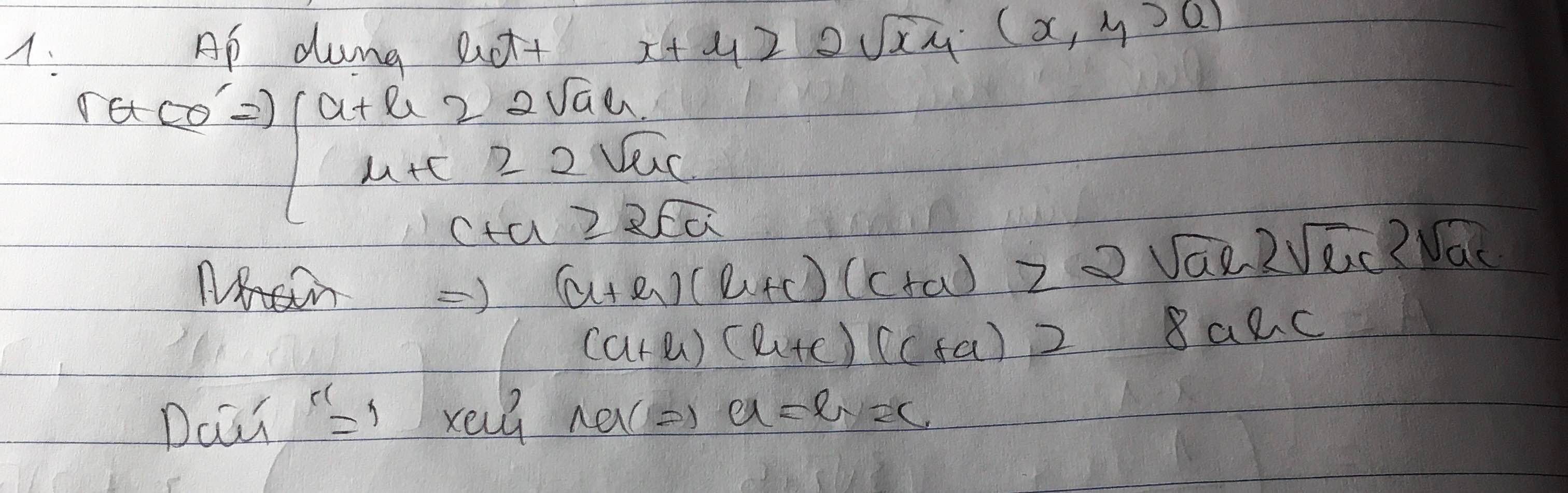Sử dụng bất đẳng thức Cô si cho hai số dương ta được
a+b\ge2\sqrt{ab}a+b≥2ab ; b+c\ge2\sqrt{bc}b+c≥2bc ; c+a\ge2\sqrt{ca}c+a≥2ca
Nhân theo vế ba bất đẳng thức này ta được đpcm.
Theo bất đẳng thức Cô si ta có : a+b ≥ \(2\sqrt{ab}\)
b+c ≥ \(2\sqrt{bc}\) , c+a ≥ \(2\sqrt{ac}\)
Nhân từng vế của 3 bất đẳng thức cho nhau ta được
(a+b)(b+c)(c+a) ≥ 8\(\sqrt{(a)^{2}(b)^{2}(c)^{2}}\)
=> (a+b)(b+c)(c+a) ≥ 8abc
theo bất đẳng thứ cô si ta có a+b >2\(\sqrt{ab}\), b+c > 2\(\sqrt{bc}\), c+a>2\(\sqrt{bc}\)
nhân tất cả ta được (a+b)(b+c)(c+a)> 8 \(\sqrt{a^2b^2c^2}\)
suy ra (a+b)(b+c)(c+a)>8abc
Sử dụng bất đẳng thức Cô si cho hai số dương ta được
a+b≥2√ab ; b+c≥2√bc ; c+a≥2√ca
Nhân theo vế ba bất đẳng thức này ta được đpcm.
Theo bất đẳng thức Cauchy, ta có:
- a + b ≥ 2\(\sqrt{ab}\)
- c + a ≥ 2\(\sqrt{ca}\)
- b + c ≥ 2\(\sqrt{bc}\)
=> (a + b)(b + c)(c + a) ≥ 8\(\sqrt{ab.bc.ac}\) = 8\(\sqrt{a^2b^2c^2}\)
Suy ra: (a + b)(b + c)(c + a) ≥ 8abc
áp dụng bdt cô - si với 2 số dương Ta có a+b ≥2\(\sqrt{ab}\)
b+c ≥ 2\(\sqrt{bc}\)
c+a ≥2\(\sqrt{ca}\)
\(\Rightarrow\) (a+b) (b+c ) ( c+a ) ≥ 8abc
Có a+b ≥ 2√a+b
b+c ≥ 2√b+c
c+a ≥ 2√c+a
=> (a+b)(b+c)(c+a)≥ (2√a+b)(2√b+c)(2√c+a)
≥ 8√a2.b2.c2
≥ 8abc
Theo bất đẳng thức Côsi ta có:
A + B ≥ 2\(\sqrt{AB}\)
B + C ≥ 2\(\sqrt{BC}\)
C + A ≥ 2\(\sqrt{AC}\)
<=> (A + B)(B + C)(C + A) ≥ 2\(\sqrt{AB}\) . 2\(\sqrt{BC}\) . 2\(\sqrt{CA}\)
<=> (A + B)(B + C)(C + A) ≥ 8ABC.
Ta có a+b≥\(2\sqrt{ab}\)
\(b+c\ge2\sqrt{bc}\)
a+c≥2\(\sqrt{ac}\)
⇒\((a+b)(a+c)(b+c)\ge2\sqrt{ab}\times2\sqrt{ac}\times2\sqrt{bc}\)=\(8abc\)(điều phải chứng minh)
Áp dụng BĐT Cô-si cho hai số dương a và b, ta có: \(a+b\ge2\sqrt{ab}\)
Tương tự, ta có: \(b+c\ge2\sqrt{bc}\) và \(c+a\ge2\sqrt{ca}\)
Nhân vế theo vế của các BĐT trên, ta được \(\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge2\sqrt{ab}.2\sqrt{bc}.2\sqrt{ca}=8\sqrt{abbcca}=8\sqrt{a^2b^2c^2}=8abc\)
Vậy với a, b, c > 0 thì
.
Áp dụng bất đẳng thức Cosi cho 3 số dương là a,b,c; có:
a+b ≥ 2 căn ab b+c ≥ 2 căn bc c+a ≥ 2 căn ca
khi đó: (a+b)(b+c)(c+a) ≥ (2 căn ab)(2 căn bc)(2 căn ca)
⇔(a+b)(b+c)(c+a) ≥ 8abc(đpcm)
vì a,b,c là các số dương theo đề bài
nên áp dụng bđt cô si ta có
a+b >= 2\(\sqrt{ab}\)
b+c >= 2\(\sqrt{bc}\)
c+a >= 2\(\sqrt{ac}\)
nhân từng vế ta được ;
(a+b)(b+c)(c+a) >= 8abc (đpcm)
Sử dụng bất đẳng thức Cô si cho hai số dương ta được
a+b≥2√aba+b≥2ab ; b+c≥2√bcb+c≥2bc ; c+a≥2√cac+a≥2ca
Nhân theo vế ba bất đẳng thức này ta được đpcm
Sử dụng bất đẳng thức Cô si cho hai số dương ta được
a+b≥2√aba+b≥2ab ; b+c≥2√bcb+c≥2bc ; c+a≥2√cac+a≥2ca
Nhân theo vế ba bất đẳng thức này ta được đpcm
Sử dụng bất đẳng thức Cô si cho hai số dương ta được
a+b≥2√aba+b≥2ab ; b+c≥2√bcb+c≥2bc ; c+a≥2√cac+a≥2ca
Nhân theo vế ba bất đẳng thức này ta được đpcm
Sử dụng bất đẳng thức Cô si cho hai số dương ta được
a+b≥2√aba+b≥2ab ; b+c≥2√bcb+c≥2bc ; c+a≥2√cac+a≥2ca
Nhân theo vế ba bất đẳng thức này ta được đpcm
Sử dụng bất đẳng thức Cô si cho hai số dương ta được
a+b≥2√aba+b≥2ab ; b+c≥2√bcb+c≥2bc ; c+a≥2√cac+a≥2ca
Nhân theo vế ba bất đẳng thức này ta được đpcm
Sử dụng bất đẳng thức Cô si cho hai số dương ta được
a+b≥2√aba+b≥2ab ; b+c≥2√bcb+c≥2bc ; c+a≥2√cac+a≥2ca
Nhân theo vế ba bất đẳng thức này ta được đpcm
Áp dụng bất đẳng thức Cô-si ta có:
a+b≥2\(\sqrt{ab}\); b+c≥2\(\sqrt{bc}\); c+a≥2\(\sqrt{ca}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge2\cdot2\cdot2\cdot\sqrt{ab}\cdot\sqrt{bc}\cdot\sqrt{ca}\)
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8abc\) (điều cần chứng minh)
Vậy \(\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8abc\)
Áp dụng BĐT Cô-si, ta có:
\(\left\{{}\begin{matrix}a+b\ge2\sqrt{ab}\\b+c\ge2\sqrt{bc}\\c+a\ge2\sqrt{ca}\end{matrix}\right.\)
Nhân vế với vế, ta sẽ có:
\(\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8abc\)
với a , b , c > 0 . Áp dụng bất đẳng thức Cô - si , ta được :
a + b
⇔Áp dụng bất đẳng thức Cô-si cho hai số a, b (a, b > 0) ,ta có:
a + b ≥ 2\(\sqrt{ab}\)
Tương tự: b + c ≥ 2\(\sqrt{bc}\)
c + a ≥ 2\(\sqrt{ca}\)
⇒ (a + b)(b + c)(c + a) ≥ 2\(\sqrt{ab}\) . 2\(\sqrt{bc}\) . 2\(\sqrt{ca}\)
⇔(a + b)(b + c)(c + a) ≥ 8abc
Dấu "=" xảy ra ⇔ a = b = c