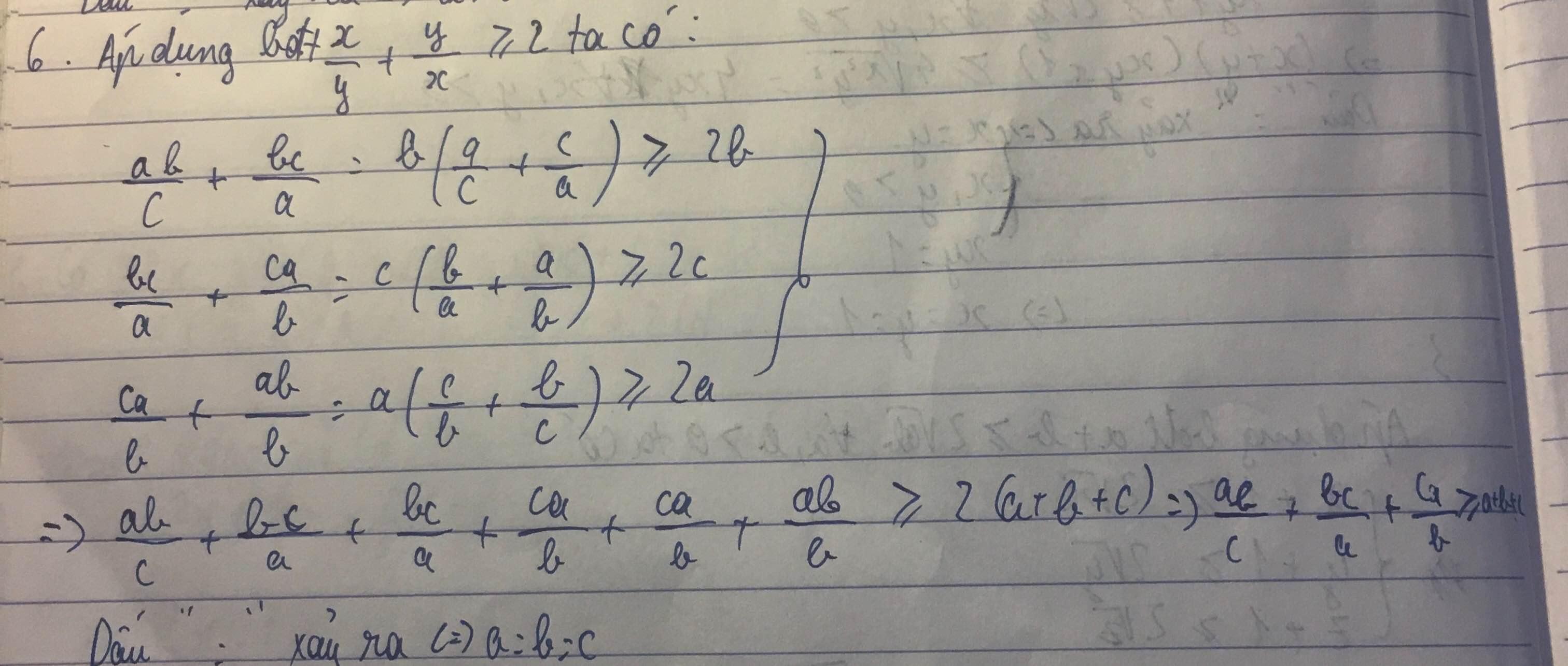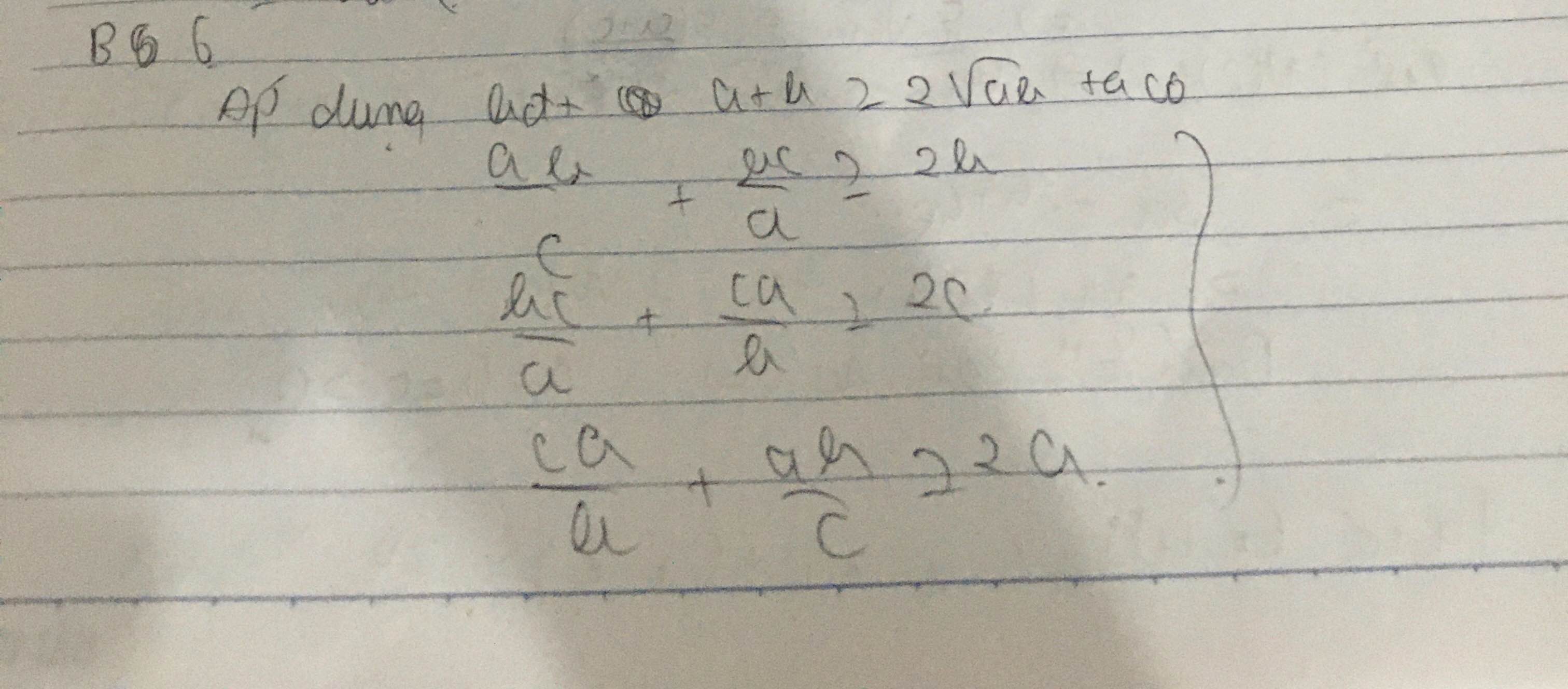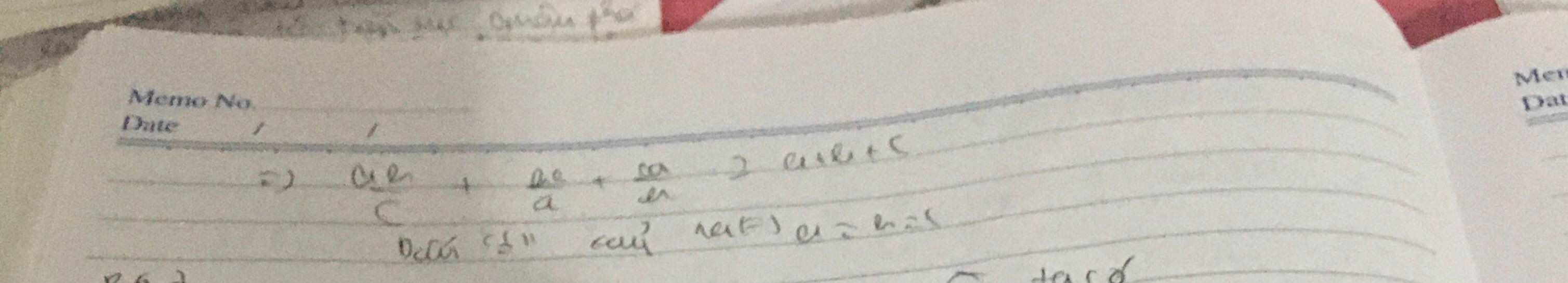Sử dụng bất đẳng thức Cô si cho 2 số dương ta có
\dfrac{ab}{c}+\dfrac{bc}{a}\ge2bcab+abc≥2b ; \dfrac{bc}{a}+\dfrac{ca}{b}\ge2cabc+bca≥2c ; \dfrac{ca}{b}+\dfrac{ab}{c}\ge2abca+cab≥2a
Cộng theo vế 3 bất đẳng thức trên rồi chia hai vế bất đẳng thức nhận được cho 2 ta được đpcm. Đẳng thức xảy ra khi và chỉ khi a=b=ca=b=c.
Áp dụng bất đẳng thức AM-GM ta có :
\(\frac{ab}{c}+\frac{bc}{a}\ge2\sqrt{\frac{ab}{c}\cdot\frac{bc}{a}}=2\sqrt{b^2}=2b\)
Tương tự : \(\frac{bc}{a}+\frac{ca}{b}\ge2c\); \(\frac{ab}{c}+\frac{ca}{b}\ge2a\)
Cộng vế với vế các bđt trên ta được đpcm
Đẳng thức xảy ra <=> a=b=c
Áp dụng bất đẳng thức cô si ta có :
\(\dfrac{ab}{c}+\dfrac{bc}{a}\)≥2b, \(\dfrac{bc}{a}+\dfrac{ac}{b}\)≥2c , \(\dfrac{ac}{b}+\dfrac{ab}{c}\)≥2a
Cộng theo vế 3 bất đẳng thức trên rồi chia hai vế bất đẳng thức nhận được cho 2 ta được đpcm. Đẳng thức chỉ xảy ra <=> a=b=c
Sử dụng bất đẳng thức Cô si cho 2 số dương ta có
; ;
Cộng theo vế 3 bất đẳng thức trên rồi chia hai vế bất đẳng thức nhận được cho 2 ta được đpcm. Đẳng thức xảy ra khi và chỉ khi .
Áp dụng BĐT Cô-si cho hai số dương \(\dfrac{ab}{c}\) và \(\dfrac{bc}{a}\), ta có; \(\dfrac{ab}{c}+\dfrac{bc}{a}\ge2\sqrt{\dfrac{ab}{c}.\dfrac{bc}{a}}=2b\)
Tương tự: \(\dfrac{bc}{a}+\dfrac{ca}{b}\ge2c;\dfrac{ab}{c}+\dfrac{ca}{b}\ge2a\)
Cộng vế theo vế của các BĐT trên, ta được:
\(\dfrac{ab}{c}+\dfrac{bc}{a}+\dfrac{bc}{a}+\dfrac{ca}{b}+\dfrac{ca}{b}+\dfrac{ab}{c}\ge2a+2b+2c\)
\(\Leftrightarrow2\left(\dfrac{ab}{c}+\dfrac{bc}{a}+\dfrac{ca}{b}\right)\ge2\left(a+b+c\right)\Leftrightarrow\dfrac{ab}{c}+\dfrac{bc}{a}+\dfrac{ca}{b}\ge a+b+c\left(đpcm\right)\)