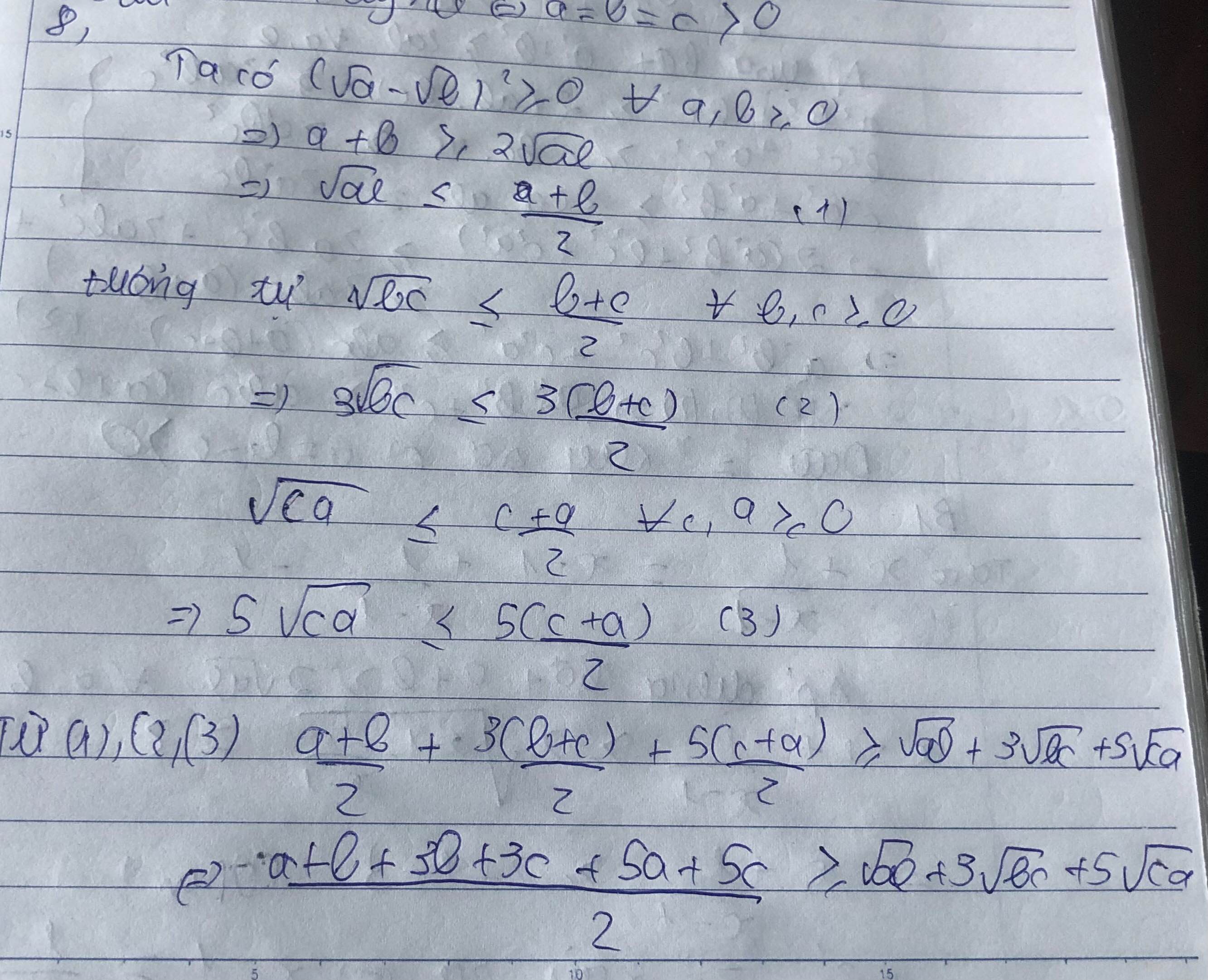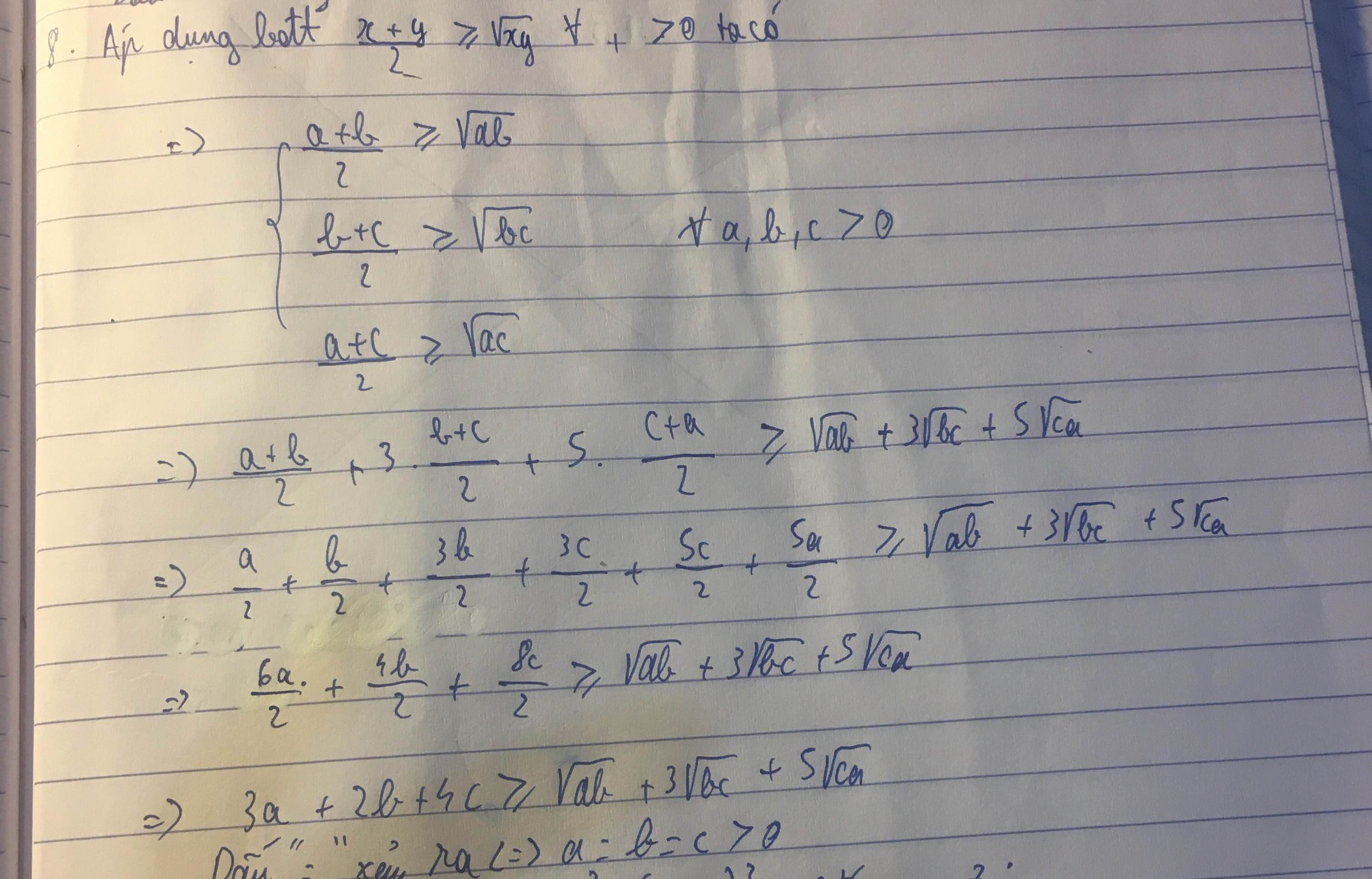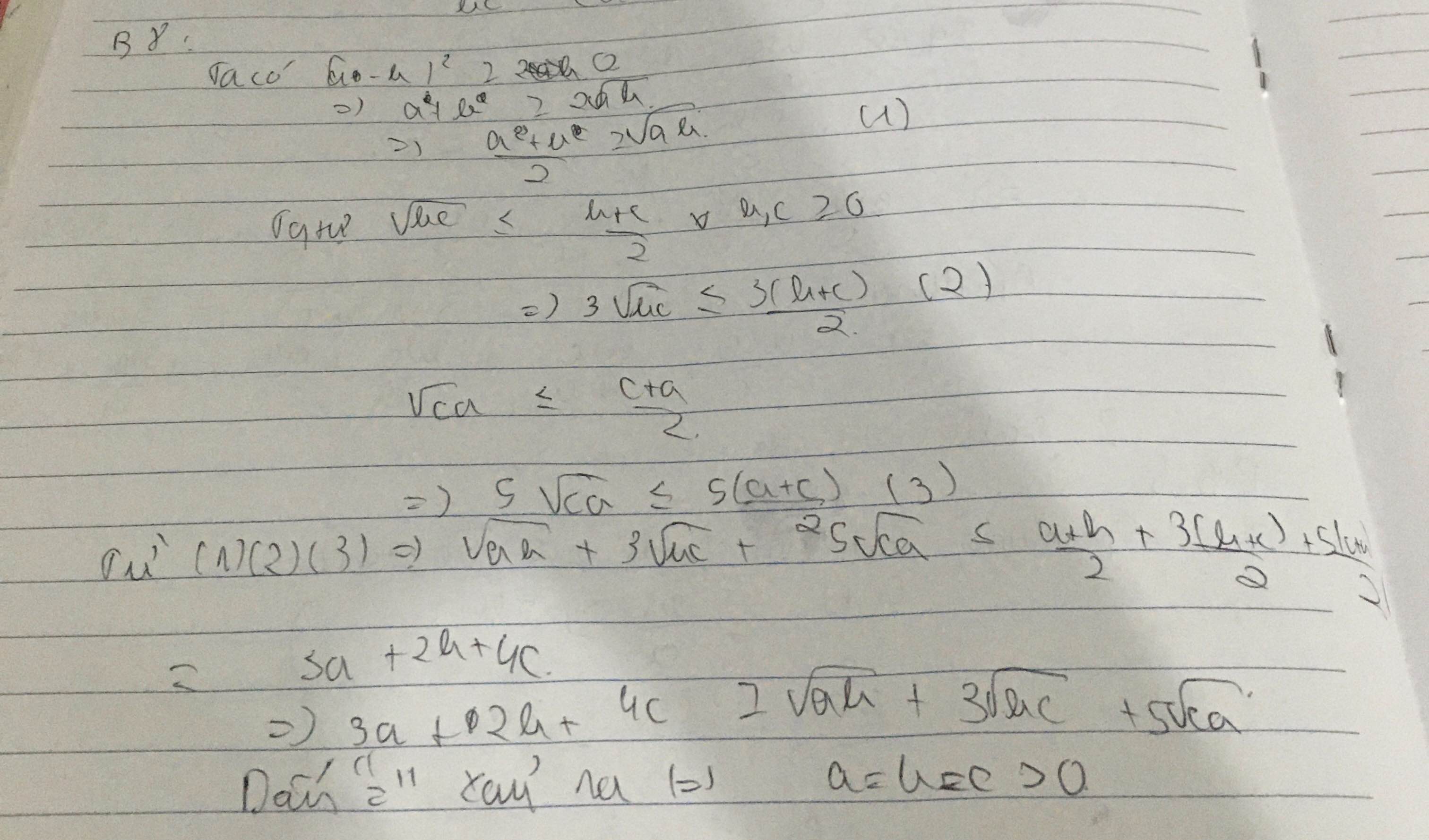Sử dụng bất đẳng thức Cô si ta có
\sqrt{ab}+3\sqrt{bc}+5\sqrt{ca}\le\dfrac{a+b}{2}+3.\dfrac{b+c}{2}+5.\dfrac{c+a}{2}ab+3bc+5ca≤2a+b+3.2b+c+5.2c+a
=3a+2b+4c=3a+2b+4c
Từ đó 3a+2b+4c\ge\sqrt{ab}+3\sqrt{bc}+5\sqrt{ca}3a+2b+4c≥ab+3bc+5ca.
Áp dụng bất đẳng thức Cô si ta được
\(\sqrt{ab}+3\sqrt{bc}+5\sqrt{ac}\) ≤ a+b/2 + 3/2*(b+c) + 5/2*(a+c) = 3a +2b+4c
<=> đpcm
Sử dụng bất đẳng thức Cô si ta có
Từ đó .