Các câu hỏi tương tự
Cho △ABC có góc B và góc C là góc nhọn, AH ⊥ BC tại H. Các khẳng định nào sau đây là sai?
A. AH < AB, AH < AC
B. HB < AB, HC < AC
C. Nếu góc HBA < góc HCA thì HB < HC
D. Nếu AB < AC thì góc HAB < góc HAC
Đề Bài: Cho tam giác ABC có AB lớn hơn AC, đường cao AH. CM: HB lớn hơn HCRồi mình giải:Vì AH vuông góc với BC suy ra:+) AB là đường xiên ứng với hình chiếu HB của tam giác ABH+) AC là đường xiên ứng với hình chiếu HC của tam giác ACHMà AB lớn hơn AC suy ra HB lớn hơn HC (Quan hệ giữa đường xiên và hình chiếu)Vậy HB lớn hơn HCTheo các bạn nếu bài này 1 điểm thì mình sẽ được bao nhiêu điểm!
Đọc tiếp
Đề Bài: Cho tam giác ABC có AB lớn hơn AC, đường cao AH. CM: HB lớn hơn HC
Rồi mình giải:
Vì AH vuông góc với BC suy ra:
+) AB là đường xiên ứng với hình chiếu HB của tam giác ABH
+) AC là đường xiên ứng với hình chiếu HC của tam giác ACH
Mà AB lớn hơn AC suy ra HB lớn hơn HC (Quan hệ giữa đường xiên và hình chiếu)
Vậy HB lớn hơn HC
Theo các bạn nếu bài này 1 điểm thì mình sẽ được bao nhiêu điểm!
Gọi H là trực tâm của tam giác nhọn ABC. Chứng minh rằng:
a) HA + HB + HC < AB + AC
b) HA + HB + HC < \(\dfrac{2}{3}\) (AB + BC + CA)
Cho hình 11, biết rằng AB < AC. Trong các kết luận sau, kết luận nào đúng? Tại sao?
a) HB = HC;
b) HB > HC;
c) HB < HC.
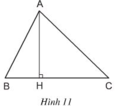
Cho tam giác ABC với AB<AC.Từ A,kẻ đg vuông góc AH đến đt BC.Trong các khẳng định sau,khẳng đinh nào đúng,sai?Tại sao?
a)HB=HC b)HB>HC c)HB<HC
Hai đường xiên AB và AC kẻ từ điểm A xuống đường thẳng BC có hình chiếu lần lượt là HB và HC. Nếu AB nhỏ hơn AC thì: A: HC>HB B: HC
Cho tam giác ABC nhọn, trức tâm H .CMR :
a, HA + HB + HB < AB + AC
b, HA + HB + HC < 2/3 ( AB + BC + CA )
Cho tam giác ABC nhọn với trực tâm H. CMR:
a) HA + HB + HC < AB+ AC
b) HA +HB + HC < 2/3(AB +BC + CA)
Cho tam giác nhọn ABC có AD và BE là hai đường cao cắt nhau tại H.
a) Cho biết góc ABC > góc ACB. Chứng minh rằng HC > HB
b) Vẽ HF vuông góc AB tại F. Chứng minh rằng ba điểm C, H, F thẳng hàng
c) Chứng minh rằng AB + AC > 2AD
d) Chứng minh rằng HA + HB + HC < 2/3 ( AB + AC + BC )
AI GIẢI NHANH VÀ ĐÚNG MIK SẼ TICK
















