Các câu hỏi tương tự
Cho tam giác ABC. Gọi M là trung điểm của BC
a) Chứng minh AM < \(\dfrac{AB+AC}{2}\)
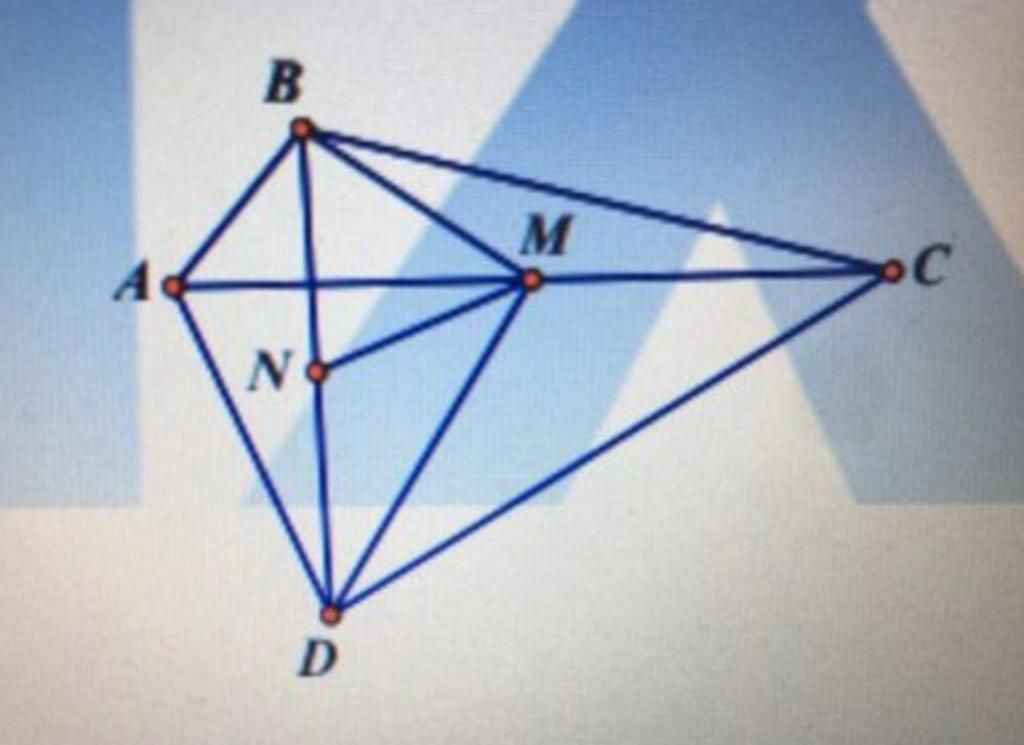
b) Cho bốn điểm A, B, C, D như hình vẽ. gọi thứ tự là trung điểm của AC và BD. Chứng minh AB+BC+CD+DA > 4.MN
Cho tam giác ABC vuông tại A(AB AC) có M là trung điểm của BC. Trên tia AM lấy điểm D sao cho AM MD. a) Chứng minh ΔAMCΔDMB . b) Chứng minh BD // AC và AD BC. c) Gọi K là trung điểm của AC. Chứng minh MK⊥BD.
Đọc tiếp
Cho tam giác ABC vuông tại A(AB < AC) có M là trung điểm của BC. Trên tia AM lấy điểm D sao cho AM = MD.
a) Chứng minh ΔAMC=ΔDMB .
b) Chứng minh BD // AC và AD = BC.
c) Gọi K là trung điểm của AC. Chứng minh MK⊥BD.
Cho tam giác ABC. Gọi M là trung điểm của BC.
a) Chứng minh A M < A B + A C 2
b) Cho bốn điểm A, B, C, D như hình vẽ. Gọi thứ tự là trung điểm của AC và BD. Chứng minh AB + BC + C + DA > 4MN
Bài 5 Cho ABC nhọn (AB<AC). Gọi D là trung điểm của AC. Trên tia đối của tia DB
lấy điểm M sao cho DB = DM.
a) Chứng minh AM = BC và AM // BC.
b) Gọi E là trung điểm AB. Trên tia đối của tia EC lấy điểm N sao cho EN = EC. Chứng
minh AN // BC và AN = BC.
c) Chứng minh M, A, N thẳng hàng và A là trung điểm của MN.
bài 4 : trên tia đối của tia AB và tia AC của ABC lấy AB'=AB, AC'=AC . chứng minh
a) BC=BC'
b) gọi M là trung điểm của BC , M' là trung điểm của B'C' . Chứng minh ba điểm M , A, M' thẳng hàng
c) AM=AM'
Cho ABC có AB AC = , lấy M là trung điểm của BC . a) Chứng minh: = ABM ACM b) Chứng minh: AM BC ⊥ c) Lấy điểm E thuộc cạnh AB , lấy điểm F thuộc cạnh AC sao cho AE AF = . Gọi I là giao điểm của EF và AM . Chứng minh: = AIE AIF và EF BC // .
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của cạnh BC. Chứng minh:
a) AM là phân giác của B A C ^
b) A M ⊥ B C .
Cho tam giác ABC có AB=AC. Gọi M là trung điểm của BC
a) Chứng minh tam giác ABM= tam giác ACM
b) Chứng minh AM vuông góc với BC
c) Gọi D là trung điểm của AC. Trên tia đối DM lấy điểm E sao cho DE=DM. Chứng minh AM song song với EC
d) Chứng minh MD=AC/.2
Cho Tam Giác ABC , Có AB= AC . Gọi M là trung điểm của BC. A) chứng minh Tam giác ABM = Tam giác ACM B) Chứng minh AM vuông góc với BC C) Gọi I là trung điểm của AM . Trên tia BI lấy điểm H sao cho BI = IH . Chứng minh AH song song với BC D) Qua M kẻ đường thẳng song song với AC cắt đường thẳng AH tại K . Chứng minh A là trung điểm của HK










