Kiến thức áp dụng
+ Số đo của góc có đỉnh bên trong đường tròn bằng một nửa tổng số đo của hai cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng một nửa số đo của cung bị chắn.
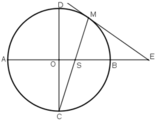
Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lây một điểm M . Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S.Chứng minh ES = EM.
Bài tập: Cho AB và CD là 2 đkinh vuông góc của đtron (o). Trên cung nhỏ BD lấy điểm M. Tiếp tuyến M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S. Chứng minh ES=EM
cho (O) và 2 đường kính AB và CD vuông góc với nhau. Trên cung BD lấy 1 điểm M. Tiếp tuyến của (O) tại M cắt AB ở E; CM cắt AB tại F . Chứng minh EF = EM
cho (O) và 2 đường kính AB và CD vuông góc với nhau. Trên cung BD lấy 1 điểm M. Tiếp tuyến của (O) tại M cắt AB ở E; CM cắt AB tại F . Chứng minh EF = EM
Cho AB và CD là hai đường kính vuông góc của đường tròn (O; R). Trên tia đối của tia CO lấy điểm S, SA cắt đường tròn (O) tại M. Tiếp tuyến tại M với đường tròn (O) cắt CD tại E, BM cắt CO tại F
a, Chứng minh: EM.AM = MF.OA
b, Chứng minh: ES = EM = EF
c, Gọi I là giao điểm của đoạn thẳng SB và (O). Chứng minh A, I, F thẳng hàng
Cho đường tròn tâm O có hai đường kính là AB và CD vuông góc với nhau tại O. Trên cung nhỏ BC lấy điểm M, AM cắt CD tại I. Tiếp tuyến của O tại M cắt tia AB tại N. Chứng minh rằng: AC là tiếp tuyến của đường tròn ngoại tiếp tam giác CMI.
Cho AB và CD là hai đường kính vuông góc của đường tròn (O; R). Trên tia đối của tia CO lấy điểm S, SA cắt đường tròn (O) tại M. Tiếp tuyến tại M với đường tròn (O) cắt CD tại E, BM cắt CO tại F
a, Chứng minh: EM.AM = MF.OA
b, Chứng minh: ES = EM = EF
c, Gọi I là giao điểm của đoạn thẳng SB và (O). Chứng minh A, I, F thẳng hàng
d, Cho EM = R, tính FA.SM theo R
e, Kẻ MH ⊥ AB. Xác định vị trí điểm M để tam giác MHO có diện tích đạt giá trị lớn nhất
Bài 4: (3,5 điểm) Cho đường tròn (O ; R) đường kính AB và điểm M bất kì thuộc đường tròn (M ≠ A, B) . Kẻ tiếp tuyến tại A của đường tròn, tiếp tuyến này cắt tia BM ở N. Tiếp tuyến của đường tròn tại M cắt AN ở D.
a) Chứng minh: 4 điểm A, D, M , O cùng thuộc một đường tròn
b) Chứng minh: OD // BM và suy ra D là trung điểm của AN
c) Đường thẳng kẻ qua O và vuông góc với BM cắt tia DM ở E. Chứng minh: BE là tiếp tuyến của đường tròn (O ; R)
d) Qua O kẻ đường thẳng vuông góc với AB và cắt đường thẳng BM tại I. Gọi giao điểm của AI và BD là J. Khi điểm M di động trên (O ; R) thì J chạy trên đường nào?
cho đường tròn tâm O bán kính R có hai đường kính AB và CD vuông góc với nhau. Trên đoạn thẳng AB lấy một điểm M (khác 0) đường thẳng CM cắt đường tròn tâm O tại điểm thứ hai N. Đường thẳng vuông góc với AB tại M cắt tiếp tuyến tại N của đường tròn ở điểm P. Chứng minh rằng:
a. Tứ giác OMNP nội tiếp được đường tròn
b. Tứ giác CMPO là hình bình hành
C. Tính CM, CN không phụ thuộc vào vị trí M
