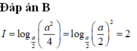Các câu hỏi tương tự
Số nào sau đây là số thực?A.
2
+
i
2
1
-
i
2
+
1
+
i
2...
Đọc tiếp
Số nào sau đây là số thực?
A. 2 + i 2 1 - i 2 + 1 + i 2 2 - i 2
B. (2 + 3i)(3 - i) + (2 - 3i)(3 + i)
C. 1 + i 2 - i 2 - i + 1 + i 2 - i 2 + i
D. 2 + i 3 2 - 2 - i 3 2
Cho a,b,c là các số thực dương,
a
≠
1
. Xét các mệnh đề sau
(
I
)
3
a
2
⇔
a
log
3
2
(
II
)
∀
x
∈
R
{
0
}
,
log
2
x
2
2
log...
Đọc tiếp
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
( I ) 3 a = 2 ⇔ a = log 3 2
( II ) ∀ x ∈ R \ { 0 } , log 2 x 2 = 2 log 2 x
( III ) log a ( bc ) = log a b . log a c
Trong ba mệnh đề (I), (II), (III) số mệnh đề sai là
A. 2
B. 3
C. 1
D. 0
Trong các khẳng định sau đây, khẳng định nào sai?A:ii là số phức thỏa mãn i^2-1i2−1.B:Số phức 2-9i2−9i có phần thực là 2 và phần ảo là -9−9.C:Số phức 2-i2−i có phần thực là 2 và phần ảo là 11.D:Phương trình x^2+1 0x2+10 có hai nghiệm trên tập số phức mathbb{C}C là ii và -i−i.
Đọc tiếp
Trong các khẳng định sau đây, khẳng định nào sai?
A:
ii là số phức thỏa mãn i^2=-1i2=−1.
B:
Số phức 2-9i2−9i có phần thực là 2 và phần ảo là -9−9.
C:
Số phức 2-i2−i có phần thực là 2 và phần ảo là 11.
D:
Phương trình x^2+1 = 0x2+1=0 có hai nghiệm trên tập số phức \mathbb{C}C là ii và -i−i.
Cho số phức z thỏa mãn
z
-
1
+
3
i
+
z
¯
+
5
+
i
2
65
Giá trị nhỏ nhất của
z
+
2
+
i...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 + 3 i + z ¯ + 5 + i = 2 65 Giá trị nhỏ nhất của z + 2 + i đạt được khi z = a + b i với a,b là các số thực dương. Giá trị của 2 a 2 + b 2 bằng
![]()
![]()
![]()
![]()
Tìm các số thực x, y thỏa mãn:
a) 2x + 1 + (1 – 2y)i = 2 – x + (3y – 2)i
b) 4x + 3 + (3y – 2)i = y +1 + (x – 3)i
c) x + 2y + (2x – y)i = 2x + y + (x + 2y)i
Cho a là số thực dương khác 1. Tính
I
log
a
a
A.
I
1
2
B. I 0 C. I -2 D. I 2
Đọc tiếp
Cho a là số thực dương khác 1. Tính I = log a a
A. I = 1 2
B. I = 0
C. I = -2
D. I = 2
Bài 1: Cho hai điểm A(1;3;5), B(1;-1;1), khi đó trung điểm I của AB có tọa độ là:
A. I(0;-4;-4).
B. I(2;2;6).
C. I(0;-2;-4).
Cho tích phân
I
∫
1
2
ln
x
x
2
d
x
b
c
+
a
ln
2
với a là số thực, b và c là các số nguyên dương, đồng thời
b
c
là phân số tối giản. Tính giá trị của biểu thức...
Đọc tiếp
Cho tích phân I = ∫ 1 2 ln x x 2 d x = b c + a ln 2 với a là số thực, b và c là các số nguyên dương, đồng thời b c là phân số tối giản. Tính giá trị của biểu thức
P = 2a + 3b + c.
A. P=6
B. P=-6
C. P=5
D. P=4
Trong không gian Oxyz cho ba điểm A (1; 2; 3), B (3; 4; 4), C (2; 6; 6) và I (a; b; c) là tâm đường tròn ngoại tiếp tam giác ABC. Tính a + b + c. A. 63/5 B. 31/3 C. 46/5 D. 10
Đọc tiếp
Trong không gian Oxyz cho ba điểm A (1; 2; 3), B (3; 4; 4), C (2; 6; 6) và I (a; b; c) là tâm đường tròn ngoại tiếp tam giác ABC. Tính a + b + c.
A. 63/5
B. 31/3
C. 46/5
D. 10