Các câu hỏi tương tự
Đồ thị hàm số
y
f
(
x
)
a
x
2
+
b
x
+
c
được cho trong hình 47. Kí hiệu
Δ
b
2
-
4
a
c
là biệt số của f(x). Trong các khẳng định sau, kh...
Đọc tiếp
Đồ thị hàm số y = f ( x ) = a x 2 + b x + c được cho trong hình 47. Kí hiệu Δ = b 2 - 4 a c là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?
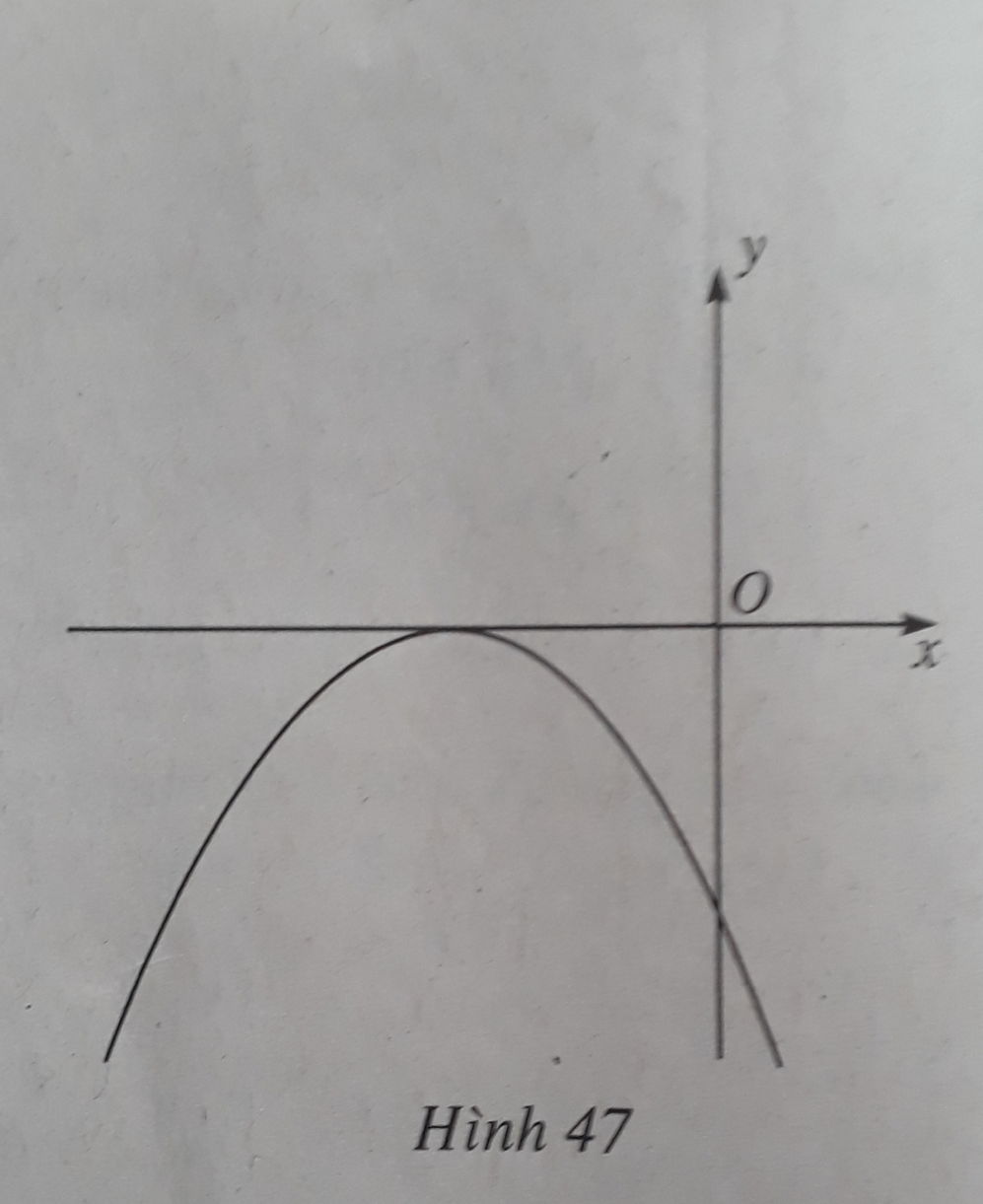
A. a, b trái dấu
B. f(x) ≤ 0, ∀x
C. a < 0, c < 0
D. Δ = 0, a < 0
Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3;1),B(4;-2) và đường thẳng d: -x+2y+1=0. a) Viết phương trình tham số của Δ đi qua A song song với đường thẳng d b) Viết phương trình tổng quát của Δ đi qua B và vuông góc với đường thẳng d c) Viết phương trình đường tròn có bán kính AB
Lập phương trình tổng quát của đường thẳng Δ trong mỗi trường hợp sau:
a) Δ đi qua M(–5; –8) và có hệ số góc k = –3;
b) Δ đi qua hai điểm A(2; 1) và B(–4; 5).
Cho đường thẳng Δ : x – y + 2 = 0 và hai điểm O(0; 0), A(2; 0).
a, Tìm điểm đối xứng của O qua Δ.
b, Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x -3 + 2t, y 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 0.a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
Đọc tiếp
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x = -3 + 2t, y = 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 = 0.
a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.
b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.
c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
Cho tam thức bậc hai f(x) = a x 2 + bx + c, (a ≠ 0) có biệt thức Δ = b 2 - 4ac. Chọn khẳng định đúng:
A. Nếu Δ < 0 thì af(x) > 0, ∀x ∈ R
B. Nếu Δ > 0 thì af(x) < 0, ∀x ∈ R
C. Nếu Δ ≤ 0 thì af(x) ≥ 0, ∀x ∈ R
D. Nếu Δ ≥ 0 thì af(x) > 0, ∀x ∈ R
Trong mặt phẳng tọa độ cho hai điểm A(3;0), B(0;2) và đường thẳng d: x + y 0.a) Lập phương trình tham số của đường thẳng Δ đi qua A và song song với db) Lập phương trình đường tròn đi qua A,B và có tâm thuộc đường thẳng dc) Lập phương trình chính tắc của elip đi qua điểm B và có tâm sai
e
5
3
Đọc tiếp
Trong mặt phẳng tọa độ cho hai điểm A(3;0), B(0;2) và đường thẳng d: x + y = 0.
a) Lập phương trình tham số của đường thẳng Δ đi qua A và song song với d
b) Lập phương trình đường tròn đi qua A,B và có tâm thuộc đường thẳng d
c) Lập phương trình chính tắc của elip đi qua điểm B và có tâm sai e = 5 3
Cho đường thẳng Δ:3x−4y+2=0.Δ:3x−4y+2=0.
a) Viết phương trình của Δ dưới dạng tham số.
b) Viết phương trình của Δ dưới dạng phương trình theo đoạn chắn.
c) Tính khoảng cách từ mỗi điểm M(3;5),N(−4;0),P(2;1)M(3;5),N(−4;0),P(2;1) tới Δ và xét xem đường thẳng cắt cạnh nào của tam giác MNP.
d) Tính góc hợp bởi Δ và mỗi trục tọa độ.
Trong mặt phẳng Oxy cho đường thẳng Δ là đồ thị của hàm số: y 1/2x.a) Tìm tung độ của hai điểm Mo và M nằm trên Δ, có hoành độ lần lượt là 2 và 6.b) Cho vectơ u→ (2; 1). Hãy chứng tỏ cùng phương với u→.
Đọc tiếp
Trong mặt phẳng Oxy cho đường thẳng Δ là đồ thị của hàm số: y = 1/2x.
a) Tìm tung độ của hai điểm Mo và M nằm trên Δ, có hoành độ lần lượt là 2 và 6.
b) Cho vectơ u→ = (2; 1). Hãy chứng tỏ 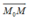 cùng phương với u→.
cùng phương với u→.






