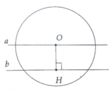
Kẻ OH ⊥ a tại H
Ta có OH=3cm < R nên a cắt (O) tại hai điểm phân biệt

Kẻ OH ⊥ a tại H
Ta có OH=3cm < R nên a cắt (O) tại hai điểm phân biệt
Cho a, b là hai đường thẳng song song và cách nhau một khoảng 2cm. Lấy điểm O trên a và vẽ đường tròn (O; 2 cm). Chứng minh đường tròn này tiếp xúc với đường thẳng b
Cho đường tròn tâm o đường kính AB. Trên đường tròn lấy một điểm I( I ko trùng vs A và B ). Tia phân giác của góc IAB cắt cung IB tại M. Lấy điểm C nằm giữa 2 điểm O và B. MC cắt đường tròn tại điểm thứ hai là E, EI cắt AM tại K
a. Chứng minh 4 điểm A,K,C,I nằm trên một đường tròn
b. Chứng minh CK song song BI
c. Từ C vẽ đường thẳng song song với AI cắt IE tại F. Gọi giao điểm của IE và AB là N. Chứng minh NB.NC = NE.NF
Cho đường tròn (O) và đường tròn (O') tiếp xúc ngoài với nhau tai A. Trên đường tròn (O) lấy điểm B sao cho ba điểm A, O, B không thẳng hàng. Đường thẳng AB cắt đưởng tròn (O') tại điểm thứ hai là C (C khác A). Chứng minh OB song song với O'C.
Cho đường tròn (O,R) và điểm A ở ngoài đường tròn với OA>2R. Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B,C là tiếp điểm). Vẽ dây BE của đường tròn (O) song song với AC;AE cắt (O) tại D khác E; BD cắt AC tại S. Gọi M là trung điểm của đoạn DE.
a) Chứng minh: A,B,C,O,M cùng thuộc một đường tròn và SC^2=SB.SD
b) Tia BM cắt (O) tại K khác B. Chứng minh: CK song song với DE.
c) Chứng minh tứ giác MKCD là một hình bình hành.
d) Hai đường thẳng DE và BC cắt nhau tại V; đường thẳng SV cắt BE tại H.
Chứng minh: Ba điểm H, O, C thẳng hàng.
Cho hai đường tròn O, O1 tiếp xúc ngoài nhau tại A. Trên đường tròn O lấy hai điểm phân biệt B, C khác A. Các đường thẳng BA, CA cắt đường tròn O1 lần lượt tại P,Q. cm PQ song song BC
Từ một điểm M ở ngoài đường tròn (O) vẽ hai tiếp tuyến MB,MD với (O) (B,D là tiếp điểm ) và một cát tuyến qua M cắt đường tròn tại hai điểm phân biệt A,C.
a)Chứng minh AB.CD=BC.AD
b)Gọi (d) là đường thẳng qua D và song song với MB:(d) cắt BA,BC lần lượt tại I;J.
Chứng minh DI=DJ
Cho đường tròn (O;R). Một đường thẳng d không đi qua O và cắt đường tròn tại hai điểm A và B. Từ một điểm C ở ngoài đường tròn; C ∈ d và CB < CA, kẻ hai tiếp tuyến CM và CN với đường tròn (M thuộc cung nhỏ AB). Gọi H là trung điểm của AB. Đường thẳng OH cắt tia CN tại K.
a) Chứng minh KN.KC = KH.KO
b) Chứng minh 5 điểm O, H, C, M, N cùng thuộc một đường tròn.
c) Đoạn thẳng CO cắt đường tròn (O) tại I. Chứng minh rằng điểm I cách đều ba cạnh của tam giác CMN.
d) Một đường thẳng đi qua O và song song với MN cắt CM và CN lần lượt tại E và F. Xác định vị trí điểm C trên d sao cho diện tích tam giác CEF nhỏ nhất
Cho các đường tròn (O; R) và (O’; R’) tiếp xúc trong với nhau tại A (R > R’). Vẽ đường kính AB của (O), AB cắt (O’) tại điểm thứ hai C. Từ B vẽ tiếp tuyến BP với đường tròn (O’), BP cắt (O) tại Q. Đường thẳng AP cắt (O) tại điểm thứ hai R. Chứng minh:
a, AP là phân giác của B A Q ^
b, CP và BR song song với nhau