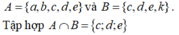Các câu hỏi tương tự
Cho các tập hợp A {a; b; c; d}; B {b; d; e}; C {a; b; e}. Trong các đẳng thức sau a. A ∩ (B C) (A ∩ B) (A ∩ C). b. A (B ∩ C) (A B) ∩ (A C). c. A ∩ (B C) (A B) ∩ (A C). d. A (B ∩ C) (A B) ∪ (A C). Số đẳng thức sai là A. 1 B. 3 C. 2 D. 4
Đọc tiếp
Cho các tập hợp A = {a; b; c; d}; B = {b; d; e}; C = {a; b; e}. Trong các đẳng thức sau
a. A ∩ (B \ C) = (A ∩ B) \ (A ∩ C).
b. A \ (B ∩ C) = (A \ B) ∩ (A \ C).
c. A ∩ (B \ C) = (A \ B) ∩ (A \ C).
d. A \ (B ∩ C) = (A \ B) ∪ (A \ C).
Số đẳng thức sai là
A. 1
B. 3
C. 2
D. 4
Bài 1:Cho các tập hợp: A={a;b;c;d}, B={a;b}. Hãy tìm tất cả tập X sao cho: B\(\cup\)X=A
Bài 2:A={a,e,i,o}, E={a,b,c,d,i,e,o,f}. Tìm CEA.
Bài 3:Cho: E={x\(\in\)N|x≤8}, A={1,3,5,7}, B={1,2,3,6}. Tìm CEA, CEB, CEA\(\cap\)CEB
Cho tập E = {a,b,c,d} ; F = {b,c,e,g} ; G = {c,d,e,f}
Chứng minh rằng
E giao(F hợp G) = (E giao F) hợp (E giao G)
Số phần tử của tập hợp A{k2+1/k ϵ Z,/k/≤2} là: A. B. C. D. Giải thích tại sao ra được đáp án.Mn giúp e giải bài này với ạ.
Đọc tiếp
Số phần tử của tập hợp A={k2+1/k ϵ Z,/k/≤2} là:
A. B.
C.
D.
Giải thích tại sao ra được đáp án.Mn giúp e giải bài này với ạ.
a)A={nϵN/n(n+1)≤15}
b)B={3k-1/kϵZ,-5≤k≤3}
c)C={xϵZ//x/<10}
d)D={xϵQ/x2-3x+1=0}
e)E={xϵZ/2x3-5x2+2x=0}
f)F={xϵN/x<20 và x chia hết cho 3}
Cho hai tập hợp
A
a
;
b
;
c
;
d
;
m
,
B
c
;
d
;
m
;
k
;
l
.
Tìm
A
∩...
Đọc tiếp
Cho hai tập hợp A = a ; b ; c ; d ; m , B = c ; d ; m ; k ; l . Tìm A ∩ B
A. A ∩ B = a ; b
B. A ∩ B = c ; d ; m
C. A ∩ B = c ; d
D. A ∩ B = a ; b ; c ; d ; m ; k ; l
1)Viết các tập hợp sau dưới dạng liệt kê các phần tử:
a)A={x N/2 <10} d)D={x Z / 9 x<26}
b)B={x Z/|x|<5} e) E={x Q/x2-x+1=0}
c)C={x R/(x+2)(x-3)(x2-5x+6)=0} f) F={3+2k/k N,k<5}
Cho tập hợp A = {a; b; c; d; e; f}. Số tập hợp con của tập hợp A là:
A. 6
B. 12
C. 64
D. 32
Bài 1. Viết lại các tập hợp sau dưới dạng liệt kê tất cả các phần tử của nó:a)A{ninN|n(n+1)le15}b)B{3k-1|kinZ, -5lekle3}c)C{xinZ||x|10}d)D{xinQ|x2-3x+10}e)E{xinZ|2x3-5x2+2x0}f)F{xinN|x20 và x chia hết cho 3}Bài 2.Viết lại các tập hợp sau bằng cách chỉra tính chất đặc trưng của chúng:a)A{1;3;5;7;...}b)B{0;2;4;6;8}c)Cleft{dfrac{1}{2};dfrac{1}{4};dfrac{1}{8};dfrac{1}{16};...right}d)D{2,6,12,20,30}e)E{-1+sqrt{3};-1-sqrt{3}}Bài 3.Hãy liệt kê các phần tử của tập hợp A gồm các số chính phương không vượ...
Đọc tiếp
Bài 1. Viết lại các tập hợp sau dưới dạng liệt kê tất cả các phần tử của nó:
a)A={n\(\in\)N|n(n+1)\(\le\)15}
b)B={3k-1|k\(\in\)Z, -5\(\le\)k\(\le\)3}
c)C={x\(\in\)Z||x|<10}
d)D={x\(\in\)Q|x2-3x+1=0}
e)E={x\(\in\)Z|2x3-5x2+2x=0}
f)F={x\(\in\)N|x<20 và x chia hết cho 3}
Bài 2.Viết lại các tập hợp sau bằng cách chỉra tính chất đặc trưng của chúng:
a)A={1;3;5;7;...}
b)B={0;2;4;6;8}
c)C=\(\left\{\dfrac{1}{2};\dfrac{1}{4};\dfrac{1}{8};\dfrac{1}{16};...\right\}\)
d)D={2,6,12,20,30}
e)E={-1+\(\sqrt{3}\);-1-\(\sqrt{3}\)}
Bài 3.Hãy liệt kê các phần tử của tập hợp A gồm các số chính phương không vượt quá 100.