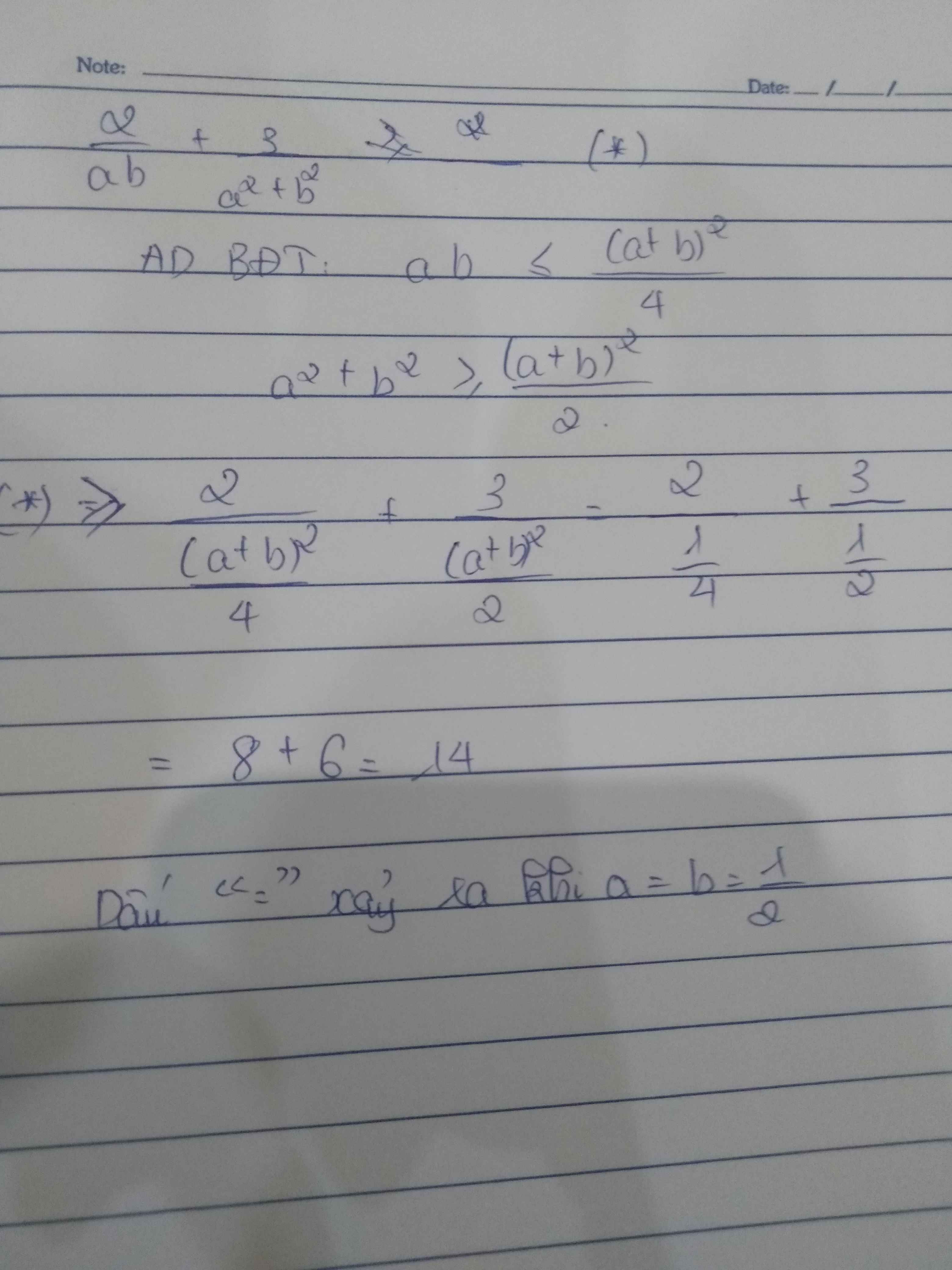Ôn tập: Bất phương trình bậc nhất một ẩn
Các câu hỏi tương tự
cho a;b;c lần lượt là các số dương thoả mãn a+b+c=3
CMR:\(\dfrac{1}{a^2+b^2+c^2}+\dfrac{2015}{ab+bc+ca}\ge672\)
Cho các số thực dương a,b,c thỏa mãn:
ab+bc+ca=3
CMR:\(\dfrac{a}{2ab^2}+\dfrac{b}{2b^2+ac}+\dfrac{c}{2cb^2+ab}>abc\)
Cho a,b,c là các số dương. Chứng minh
a) a2+b2≥ 2ab
b) ab2/(a2+b2) + bc2/(b2+c2) +ca2/(c2+a2) ≤ (a+b+c)/2
a)Chứng tỏ rằng: \(\frac{a^2}{x}+\frac{b^2}{y}\ge\frac{\left(a+b\right)^2}{x+y}\) với mọi giá trị dương của a,b,x,y
b) Chứng tỏ rằng: \(\frac{a^3}{b}+\frac{b^3}{c}+\frac{c^3}{a}\ge ab+bc+ca\) với a,b,c dương
29 tháng 3 2022 lúc 21:45
Bài toán 1. Cho a, b, c là các số thực dương thỏa mãn $latex a+b+c=3$. Chứng minh rằng
$latex \frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}+\frac{\text{2}\left( {{a}^{\text{2}}}+{{b}^{2}}+{{c}^{2}} \right)}{3}\ge 5$
A. Cho a vs b là các số dương , chứng tỏ :
a. \(\frac{a+b}{2}\)> hoặc = căn bậc a nhân b
b. a/b + b/a > hoặc = 2
B. Tìm giá trị nhỏ nhất của biểu thức :
a. A= x2 + 2
b. B= x2 +4x + 12
c. C= 9x2 - 6x + 10
Cho a,b,c là các số dương và a+b+c = 3. CM :
B= \(\frac{a}{1+b^2}+\frac{b}{1+c^2}+\frac{c}{1+a^2}\ge\frac{3}{2}\)
1. Chứng minh rằng với mọi số thực không âm x, y ta luôn có: x3 + y3 > x2y + xy2
2. Tìm x sao cho giá trị của biểu thức 111(x-2) không nhỏ hơn 1998
3. Cho 2 số dương a và b , biết a > 2b: Chứng minh: \(\frac{a-b}{b}\) >1
4.Chứng minh bất đẳng thức sau : x2 + y2 + z2 + 14 > 4x - 2y -6z
Cho a, b, c là các số dương và \(a^2+b^2+c^2=1\). Tìm GTNN của
P= \(\frac{bc}{a}+\frac{ac}{a}+\frac{ab}{c}\)