Các câu hỏi tương tự
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) f(x)
(
25
-
x
2
)
trên đoạn [-4; 4]b) f(x) |
x
2
– 3x + 2| trên đoạn [-10; 10]c) f(x) 1/sinx trên đoạn [π/3; 5π/6]d) f(x) 2sinx + sin2x trên đoạn [0; 3π/2]
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
Cho hàm số \(f\left(x\right)\) có đạo hàm bằng \(f'\left(x\right)=x^2\left(x-1\right)^3\left(x-2\right)\) . Số điểm cực trị của hàm số \(f\left(x\right)\) bằng:
A.0 B.1 C.2 D.3
Cho hàm số y = f(x) liên tục trên R sao cho maxf(x) = f(2) = bằng 84 trên [0; 10] . Xét hàm số g(x) = f(x3+x) - x2 + 2x + m.Tìm m để giá trị lớn nhất của g(x) trên [0; 2]
Cho hai hàm số yf(x),yg(x) có đạo hàm là f(x),g(x) Đồ thị hàm số f(x), g(x) được cho như hinh vẽ dưới đây Biết rằng f(0)-f(6)g(0)-g(6) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số h(x)f(x)-g(x) trên đoạn [0;6] lần lượt là: A. h(6),h(2) B. h(0),h(2) C. h(2),h(6) D. h(2),h(0)
Đọc tiếp
Cho hai hàm số y=f(x),y=g(x) có đạo hàm là f'(x),g'(x) Đồ thị hàm số f'(x), g'(x) được cho như hinh vẽ dưới đây
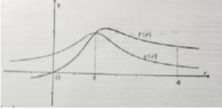
Biết rằng f(0)-f(6)<g(0)-g(6) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [0;6] lần lượt là:
A. h(6),h(2)
B. h(0),h(2)
C. h(2),h(6)
D. h(2),h(0)
Cho hàm số y f(x) có đạo hàm f(x). Hàm số y f(x) liên tục trên tập số thực và có bảng biến thiên như sau: Biết rằng f(-1)
10
3
, f(2) 6. Giá trị nhỏ nhất của hàm số g(x)
f
3
(
x
)
-
3
f
(
x
)
trên đoạn [-1;2] bằng A.
10
3
B.
820
27...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f'(x). Hàm số y = f'(x) liên tục trên tập số thực và có bảng biến thiên như sau:
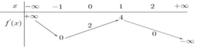
Biết rằng f(-1) = 10 3 , f(2) = 6. Giá trị nhỏ nhất của hàm số g(x) = f 3 ( x ) - 3 f ( x ) trên đoạn [-1;2] bằng
A. 10 3
B. 820 27
C. 730 27
D. 198
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) 0, F(2) 1, G(2) 1 và
∫
0
2
F
(
x
)
g
(
x
)
d
x
3 . Tính tích phân hàm:
∫
0
2
G
(
x
)
f
(
x
)
d
x
A. I 3. B. I 0....
Đọc tiếp
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và ∫ 0 2 F ( x ) g ( x ) d x = 3 . Tính tích phân hàm: ∫ 0 2 G ( x ) f ( x ) d x
A. I = 3.
B. I = 0.
C. I = -2.
D. I = -4.
Cho hai hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
-
1
2
và
g
(
x
)
d
x
2
+
e
x
+
1
(
a
,
b
,
c
,
d...
Đọc tiếp
Cho hai hàm số f ( x ) = a x 3 + b x 2 + c x - 1 2 và g ( x ) = d x 2 + e x + 1 ( a , b , c , d , e ∈ ℝ ) . Biết rằng đồ thị của hàm số y = f(x) và y = g(x) cắt nhau tại ba điểm có hoành độ lần lượt là –3; –1;1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
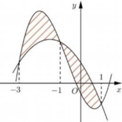
A. 9 2
B. 8
C. 4
D. 5
Giả sử F(x) là một nguyên hàm của
f
(
x
)
ln
(
x
+
3
)
x
2
sao cho F(-2)+F(1)0. Giá trị của F(-1)+F(2) bằng B. 0
Đọc tiếp
Giả sử F(x) là một nguyên hàm của f ( x ) = ln ( x + 3 ) x 2 sao cho F(-2)+F(1)=0. Giá trị của F(-1)+F(2) bằng
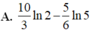
B. 0
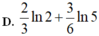
cho h/s y = f(x) liên tục trên R sao cho gtln cùa f(x) trên [-1;2] bằng 3. Xét g(x) = f(3x - 1) + m. Tìm m để gtln của g(x) bằng -10 trên doan [0;1]