\(a,P=\dfrac{3\sqrt{x}+6+x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\left(x\ge0;x\ne9;x\ne4\right)\\ P=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{1}{\sqrt{x}+3}=\dfrac{1}{\sqrt{x}-2}\\ b,P< 0\Leftrightarrow\sqrt{x}-2< 0\left(1>0\right)\\ \Leftrightarrow0\le x< 4\)
Đúng 1
Bình luận (1)
Các câu hỏi tương tự
Chỉ em vs ạ em ko bt làm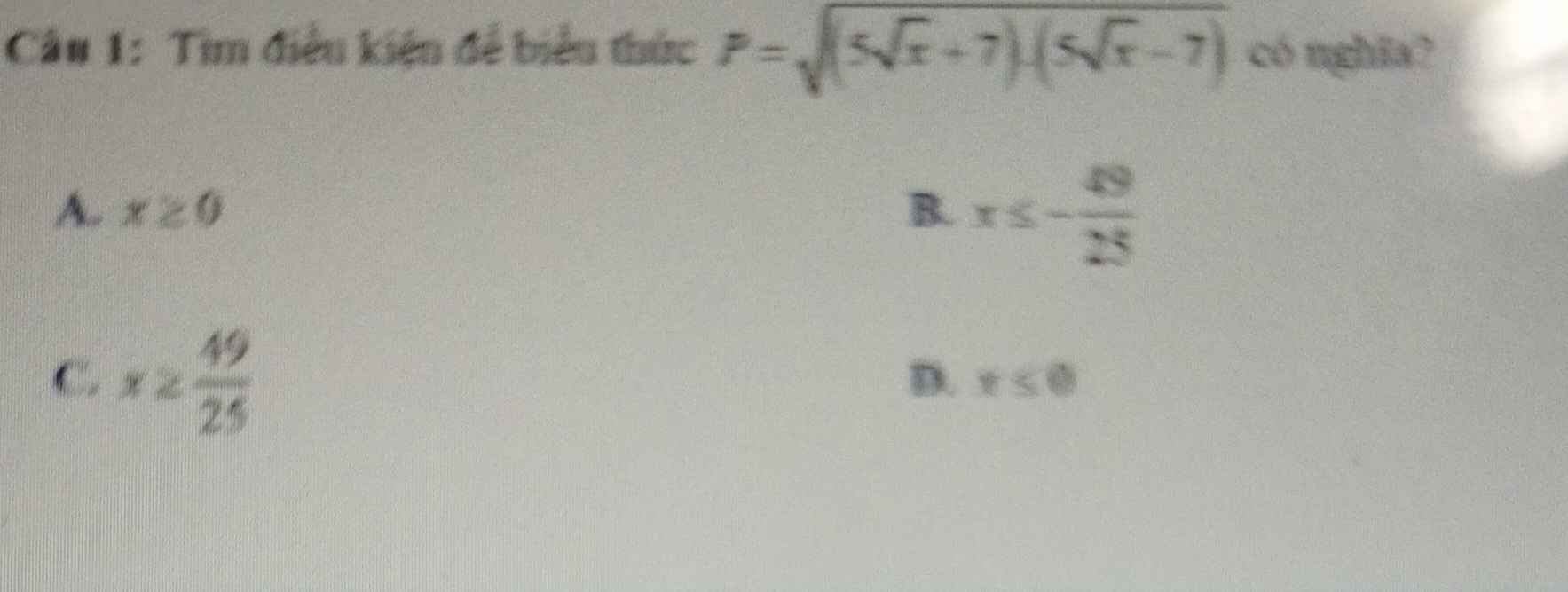
làm giúp em bài này đc ko ạ. Em cảm ơn ạ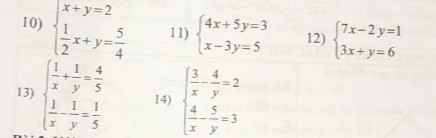
Làm giúp em 2bài này đc ko ạ. Em cảm ơ ạ
giúp em bài này gấp vơi ạ huhu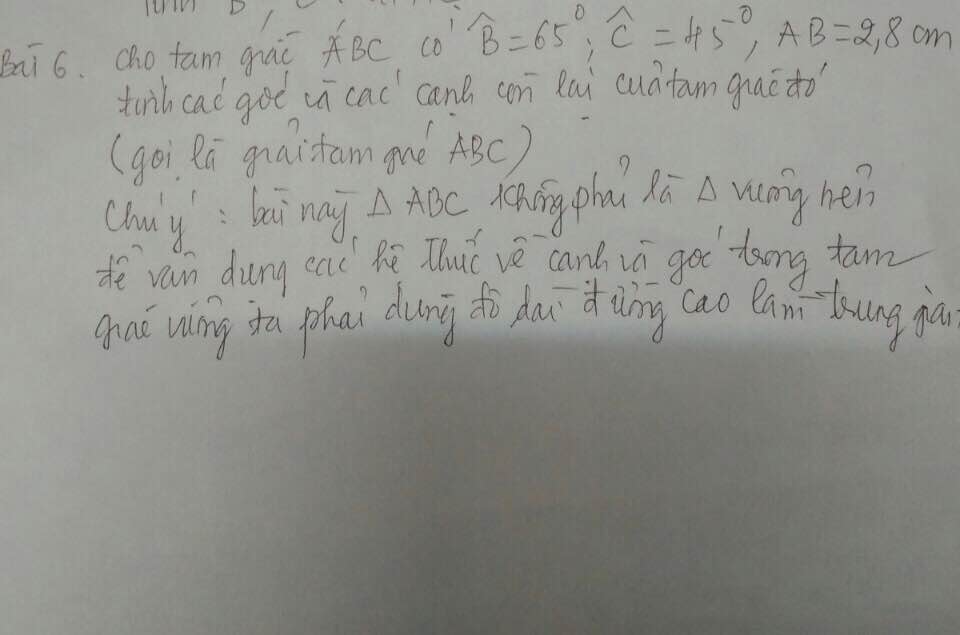
\(\sqrt{5-x}+\sqrt{x-1}=-x^2+2x+1\)
Nhờ các anh chị giúp em cách làm với e bt kết quả là 1 nhưng ko bt làm NTN?
cảm ơn lun
Làm giúp em câu b được ko ạ. Em cảm ơn nhiều ạ
Làm giúp em bài này được ko ạ. Em cảm ơn nhìu ạ
Giúp em, xem em làm đúng ko ạ
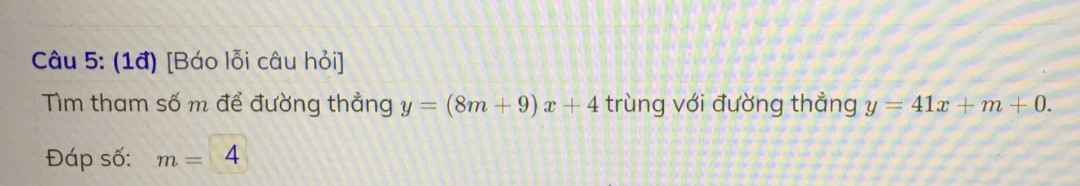
Làm nhanh giúp em với ạ chỉ công thức cho em luôn với ạ










