Đề bài là \(\left|\overrightarrow{MD}+2\overrightarrow{MA}+3\overrightarrow{MC}\right|=\left|\overrightarrow{MB}-\overrightarrow{MD}\right|\) đúng ko nhỉ?
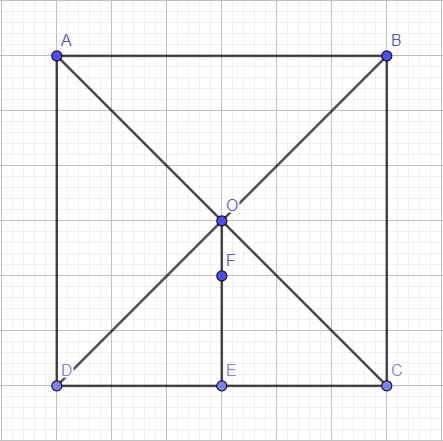
Gọi E là trung điểm CD, O là tâm hình vuông, F là điểm thuộc OE sao cho \(\overrightarrow{FE}+2\overrightarrow{FO}=\overrightarrow{0}\)
Theo tính chất trung tuyến: \(\left\{{}\begin{matrix}\overrightarrow{MD}+\overrightarrow{MC}=2\overrightarrow{ME}\\\overrightarrow{MA}+\overrightarrow{MC}=2\overrightarrow{MO}\end{matrix}\right.\)
Do đó:
\(\left|\overrightarrow{MD}+\overrightarrow{MC}+2\left(\overrightarrow{MA}+\overrightarrow{MC}\right)\right|=\left|\overrightarrow{MB}+\overrightarrow{DM}\right|\)
\(\Leftrightarrow\left|2\overrightarrow{ME}+4\overrightarrow{MO}\right|=\left|\overrightarrow{DB}\right|\)
\(\Leftrightarrow2\left|\overrightarrow{MF}+\overrightarrow{FE}+2\overrightarrow{MF}+2\overrightarrow{FO}\right|=DB\)
\(\Leftrightarrow2\left|3\overrightarrow{MF}+\overrightarrow{FE}+2\overrightarrow{FO}\right|=DB\)
\(\Leftrightarrow6\left|\overrightarrow{MF}\right|=DB\)
\(\Leftrightarrow MF=\dfrac{DB}{6}=\dfrac{a\sqrt{2}}{6}\)
Vậy tập hợp M là đường tròn tâm F bán kính \(\dfrac{a\sqrt{2}}{6}\)