\(\dfrac{2bz-3cy}{a}=\dfrac{3cx-az}{2b}=\dfrac{ay-2bx}{3c}\)
\(\Leftrightarrow\dfrac{2abz-3acy}{a^2}=\dfrac{6bcx-2abz}{4b^2}=\dfrac{3acy-6bcx}{9c^2}\)
\(=\dfrac{2abz-3acy+6bcx-2abz+3acy-6bcx}{a^2+4b^2+9c^2}=0\)
\(\Rightarrow2bz-3cy=0\Rightarrow\dfrac{z}{3c}=\dfrac{y}{2b}\left(1\right)\)
\(\Rightarrow3cx-az=0\Rightarrow\dfrac{x}{a}=\dfrac{z}{3c}\left(2\right)\)
Từ (1) và (2) suy ra: \(\dfrac{x}{a}=\dfrac{y}{2b}=\dfrac{z}{3c}\)

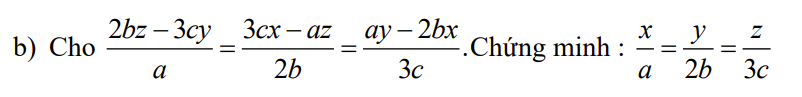





 Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé
Giúp dùm mik câu b với ạ!! Vẽ hình câu b giúp mik luôn nhé






