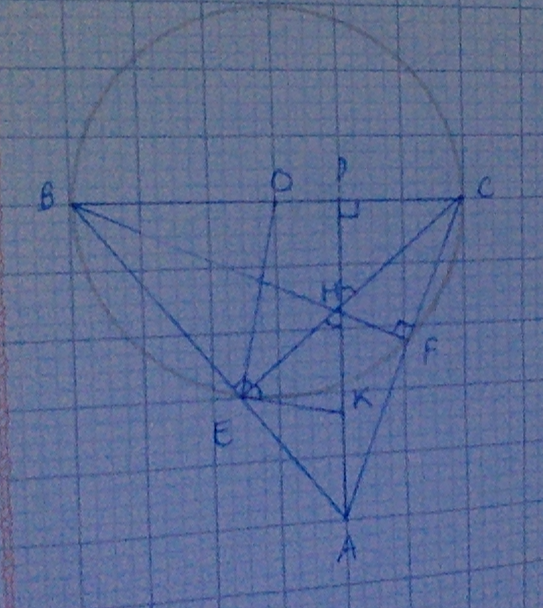
Câu 5 Cho ∆ABC nhọn, đường tròn (O) đường kính BC cat AB, A và F. Gọi H là giao điểm của BF và CE, AH cắt BC tại D. a) Chứng minh: AH vuông góc với BC và tứ giác AEHF nội tiếp, xác định tâm K của đường tròn này. b) Chứng minh: KE là tiếp tuyến của đường tròn (O) và năm điểm O, D, E, K, F cùng thuộc một đường tròn. c) Qua H vẽ đường thẳng vuông góc HO cắt AB, AC lần lượt tại M và N. Chứng minh: HN = ΗΝ.
Sửa đề: Đường tròn đường kính BC cắt AB, AC tại E và F
a) (O) có \(\widehat{BEC},\widehat{BFC}\) là 2 góc nội tiếp chắn nửa đường tròn nên \(\widehat{BEC}=90^o,\widehat{BFC}=90^o\Rightarrow CE\perp AB,BF\perp AC\). CE cắt BF tại H nên H là trực tâm của \(\Delta ABC\) => AH là đường cao thứ 3 => \(AH\perp BC\)
\(\widehat{BEC}=90^o\Rightarrow\widehat{AEH}=90^o.\widehat{BFC}=90^o\Rightarrow\widehat{AFH}=90^o\)
Tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^o+90^o=180^o\) nên nội tiếp.
Đường tròn ngoại tiếp tứ giác AEHF là đtron ngoại tiếp \(\Delta AEH\). \(\Delta AEH\) vuông tại E (\(\widehat{AEH}=90^o\)) nên tâm K của đường tròn này là trung điểm AH.
b) \(\Delta AEH\) vuông tại E có EK là trung tuyến (K là trđ AH) nên EK = AH/2 = KH = KA.
EK = KH nên \(\Delta EKH\) cân tại K => \(\widehat{KEH}=\widehat{KHE}\). Mà \(\widehat{KHE}=\widehat{DHC}\) (đối đỉnh) nên \(\widehat{KEH}=\widehat{DHC}\) (1)
\(\Delta OEC\) cân tại O (OE = OC = R) nên \(\widehat{OEC}=\widehat{OCE}=\widehat{HCD}\) (2)
\(\Delta DHC\) vuông tại D (\(AH\perp BC\)) nên \(\widehat{DHC}+\widehat{HCD}=90^o\) (3)
Từ (1), (2), (3) => \(\widehat{KEH}+\widehat{OEC}=90^o\Rightarrow\widehat{OEK}=90^o\Rightarrow OE\perp EK\). Lại có \(E\in\left(O\right)\) nên EK là tiếp tuyến của (O).