Question

Câu 2: Cho hình thang ABCD, 2 đáy AB và CD. Đường thẳng song song với đáy AB cắt các cạnh bên và đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M N P Q. Giao của 2 đường chéo là O

Chứng minh rằng:

a) OA.OD=OB.OC

b) MN=PQ
giải nhanh giúp mik với ạ

Answer 1

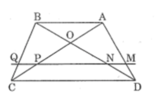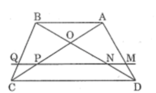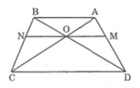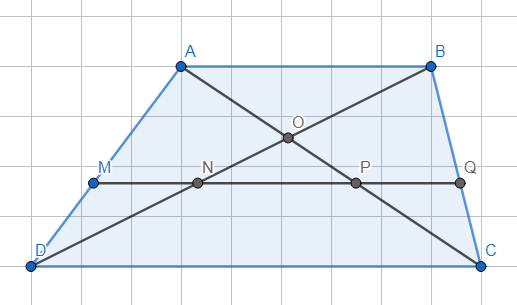
a) △OAB có: AB//CD.

\(\Rightarrow\dfrac{OA}{OC}=\dfrac{OB}{OD}\) (định lí Ta-let) \(\Rightarrow OA.OD=OB.OC\).

b) △ADB có: MN//AB.

\(\Rightarrow\dfrac{MN}{AB}=\dfrac{DM}{DA}\) (hq định lí Ta-let) (1)

△ACB có: PQ//AB.

\(\Rightarrow\dfrac{PQ}{AB}=\dfrac{CP}{CA}\) (hq định lí Ta-let) (2)

△ADC có: MP//DC.

\(\Rightarrow\dfrac{DM}{DA}=\dfrac{CP}{CA}\) (định lí Ta-let) (3).

Từ (1), (2), (3) suy ra: \(\dfrac{MN}{AB}=\dfrac{PQ}{AB}\Rightarrow MN=PQ\)