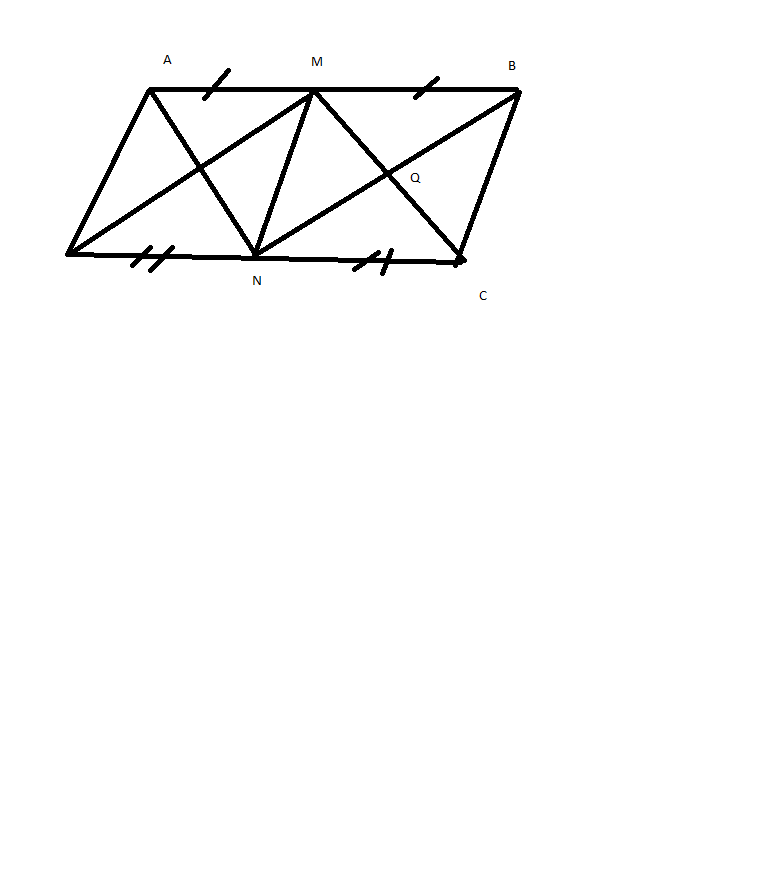
a) Vì ABCD là hình bình hành nên
AB=CD=2a, AD=BC=a
ta có: M,N là trung điểm của AB và CD
=> DN=1/2CD=a
=> AD=DN
Vậy tam giác ADN cân tại D(đpcm)
=> DAN=DNA
b) Ta có: AB//CD => AND=MAN(So le trong)
=> DAN=MAN
=>AN là tia phân giác của góc BAD
c) Chứng minh tương tự câu B ta được:
AMCN là hình bình hành (vì AM//CN, AM=CN)
=>AN//CM=> PN//MQ
Ta có: BMND là hình bình hành (chứng minh b)
=>DM//BN => MP//NQ
=> MPNQ là hình bình hành(1)
Ta có: AM//DN,AM=DN=a
=> AMND là hình bình hành
mặt khác AD=AN(chứng minh a)
=>AMND là hình thoi
=> AN vuông góc với DM(tính chất 2 đường chéo của hình thoi)
=> MPN= 90 độ (2)
Từ (1) và (2) suy ra PMQN là hình chữ nhật ( dấu hiệu: hbh có 1 góc vuông là hcn)
giải mấy bài này mình đủ mệt não rồi bạn ơi ![]()