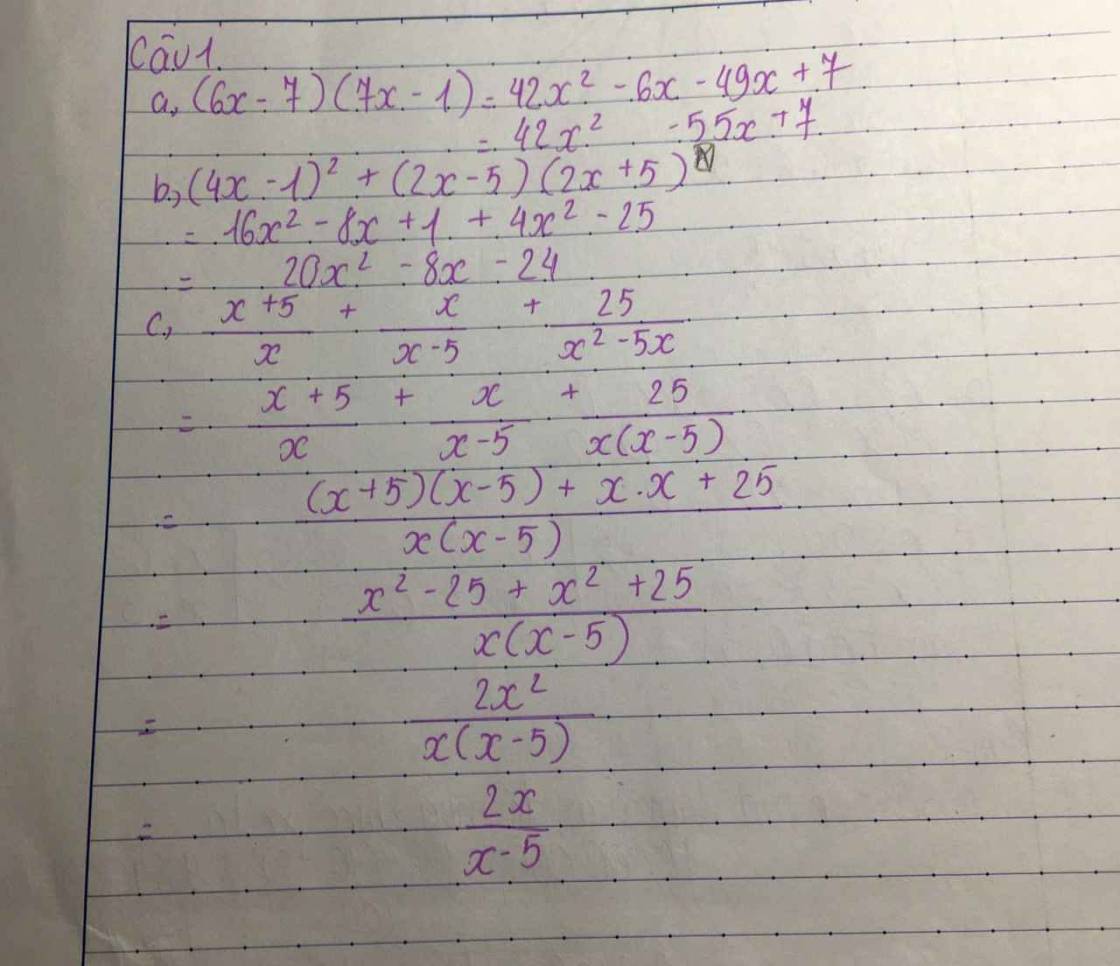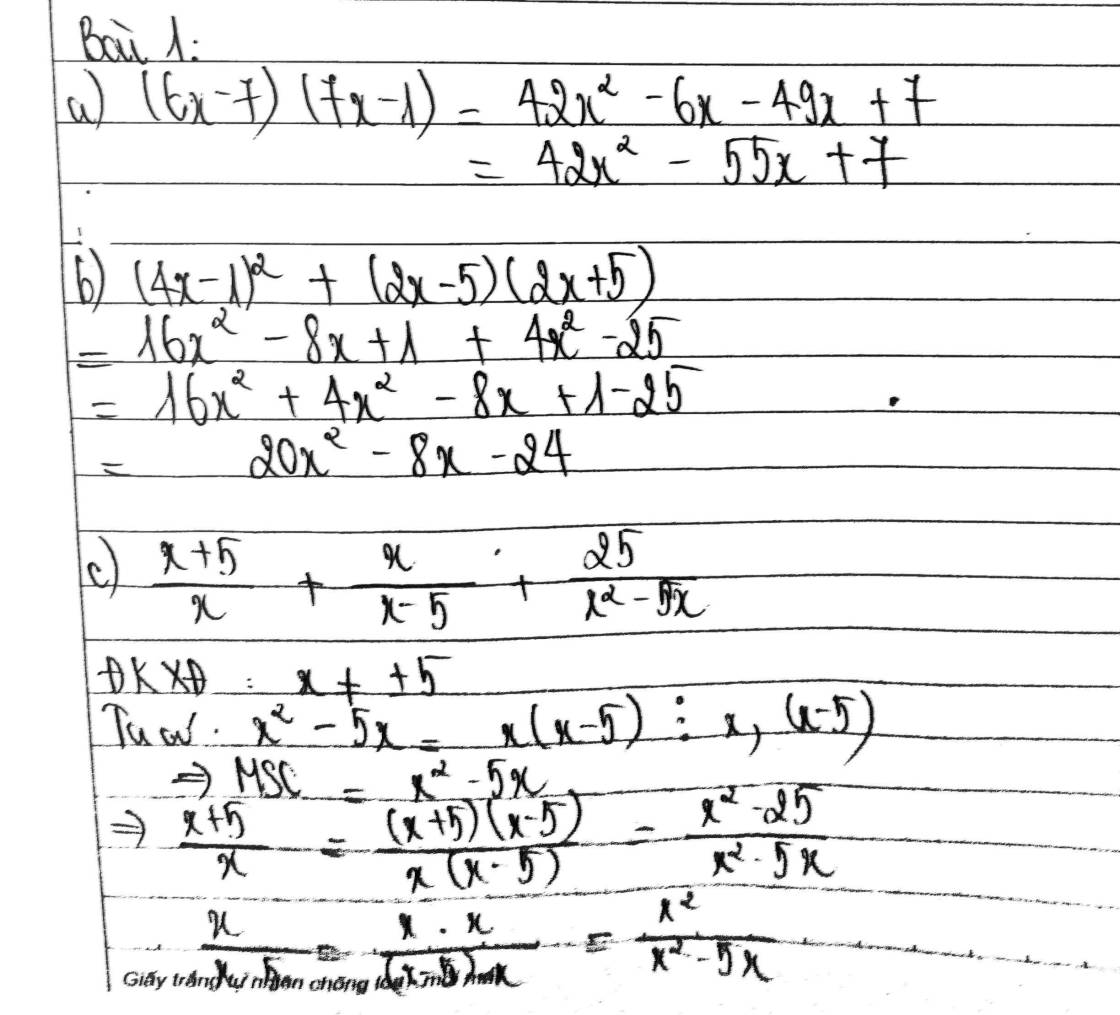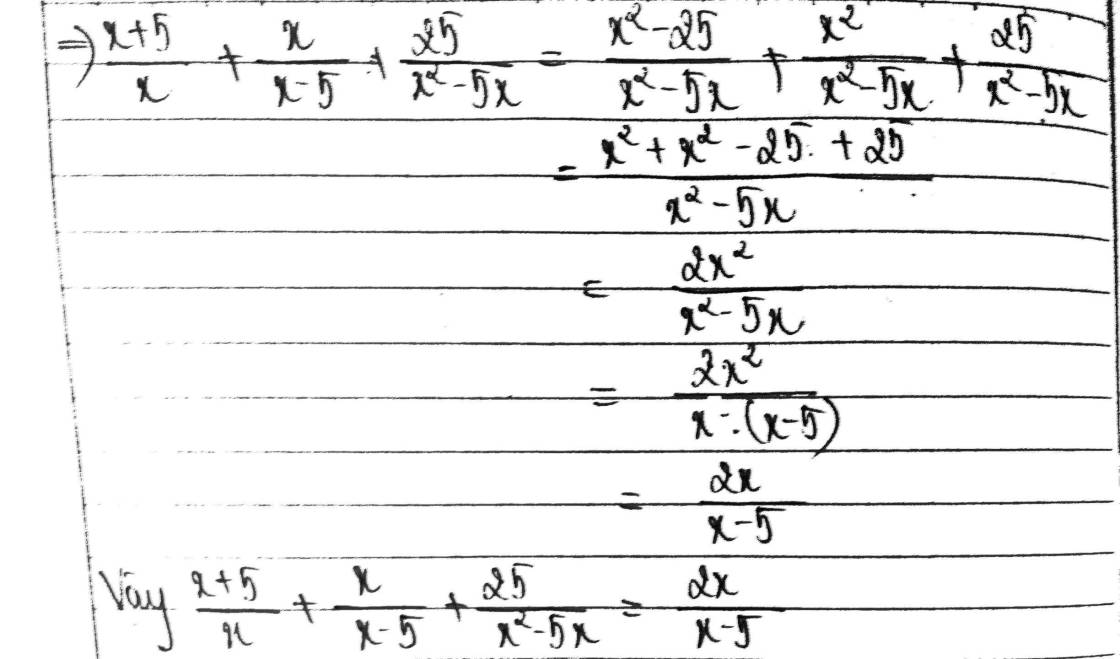\(a,\\ \left(6x-7\right).\left(7x-1\right)=6x.7x-7x.7-6x.1-7.\left(-1\right)\\ =42x^2-49x-6x+7=42x^2-55x+7\\ b,\\ \left(4x-1\right)^2+\left(2x-5\right).\left(2x+5\right)=16x^2-8x+1+4x^2-25\\ =20x^2-8x-24\)
\(c,\\ \dfrac{x+5}{x}+\dfrac{x}{x-5}+\dfrac{25}{x^2-5x}\\ =\dfrac{\left(x-5\right).\left(x+5\right)}{x.\left(x-5\right)}+\dfrac{x.x}{x.\left(x-5\right)}+\dfrac{25}{x.\left(x-5\right)}\\ =\dfrac{x^2-25+x^2+25}{x.\left(x-5\right)}=\dfrac{2x^2}{x.\left(x-5\right)}=\dfrac{2x}{\left(x-5\right)}\left(ĐK:x\ne0;x\ne5\right)\)
a) (6x-7)(7x-1)
=42x2-6x-49x+1
=42x2-55x+1
b) (4x-1)2 + (2x - 5)(2x +5)
= 16x2 - 8x + 1 + 4x2 - 25
= 20x2 - 8x - 24
c) x+5/x +x/x-5 + 25/x2 - 5x
= x + 5/x + x/x-5 + 25/x( x - 5)
= (x+5)(x-5)/x(x-5)+x.x/x(x-5)+25/x(x-5)
= x2-25+x2+25/x(x-5)
= 2x2/x(x-5)
a,
(6x−7).(7x−1)=6x.7x−7x.7−6x.1−7.(−1)
=42x
2
−49x−6x+7=42x
2
−55x+7
b,
(4x−1)
2
+(2x−5).(2x+5)=16x
2
−8x+1+4x
2
−25
=20x
2
−8x−24
c,\\ \dfrac{x+5}{x}+\dfrac{x}{x-5}+\dfrac{25}{x^2-5x}\\ =\dfrac{\left(x-5\right).\left(x+5\right)}{x.\left(x-5\right)}+\dfrac{x.x}{x.\left(x-5\right)}+\dfrac{25}{x.\left(x-5\right)}\\ =\dfrac{x^2-25+x^2+25}{x.\left(x-5\right)}=\dfrac{2x^2}{x.\left(x-5\right)}=\dfrac{2x}{\left(x-5\right)}\left(ĐK:x\ne0;x\ne5\right)c,
x
x+5
+
x−5
x
+
x
2
−5x
25
=
x.(x−5)
(x−5).(x+5)
+
x.(x−5)
x.x
+
x.(x−5)
25
=
x.(x−5)
x
2
−25+x
2
+25
=
x.(x−5)
2x
2
=
(x−5)
2x
(ĐK:x
=0;x
=5)
a) (6x -7)(7x -1)=42x2-6x-49x+1=42x2-55x+1
b)
a ( 6x - 7 )( 7x - 1)
42x^2 - 6x - 49x + 7
42^2 - 55x + 7
b ( 4x -1 )^2 + ( 2x -5)(2x + 5)
4x^2 - 8x + 1 + 4x^2 + 10x - 10x -25
8x^2 - 8x - 24