\(\left[{}\begin{matrix}M+N=5x^2+xyz-5xy+3-y+3xyz-3x^2+5xy-1=2x^2+4xyz+2-y\\M-N=3xyz-3x^2+5xy-1-5x^2-xyz+5xy-3+y=2xyz-8x^2+10xy-4+y\\N-M=5x^2+xyz-5xy+3-y-3xyz+3x^2-5xy+1=8x^2-2xyz-10xy+4-y\end{matrix}\right.\)
\(M+N=\left(3xyz-3x^2+5xy-1\right)+\left(5x^2+xyz-5xy+3-y\right)\)
\(=3xyz-3x^2+5xy-1+5x^2+xyz-5xy+3-y\)
\(=\left(3xyz+xyz\right)+\left(-3x^2+5x^2\right)+\left(5xy-5xy\right)+\left(-1+3\right)+\left(-y\right)\)
\(=4xyz+2x^2+2-y\)
\(M-N=\left(3xyz-3x^2+5xy-1\right)-\left(5x^2+xyz-5xy+3-y\right)\)
\(=3xyz-3x^2+5xy-1-5x^2-xyz+5xy-3+y\)
\(=\left(3xyz-xyz\right)+\left(-3x^2-5x^2\right)+\left(5xy+5xy\right)+\left(-1-3\right)+y\)
\(=2xyz-8x^2+10xy-4+y\)
\(N-M=\left(5x^2+xyz-5xy+3-y\right)-\left(3xyz-3x^2+5xy-1\right)\)
\(=5x^2+xyz-5xy+3-y-3xyz+3x^2-5xy+1\)
\(=\left(5x^2+3x^2\right)+\left(xyz-3xyz\right)+\left(-5xy-5xy\right)+\left(3+1\right)+\left(-y\right)\)
\(=8x^2-2xyz-10xy+4-y\)
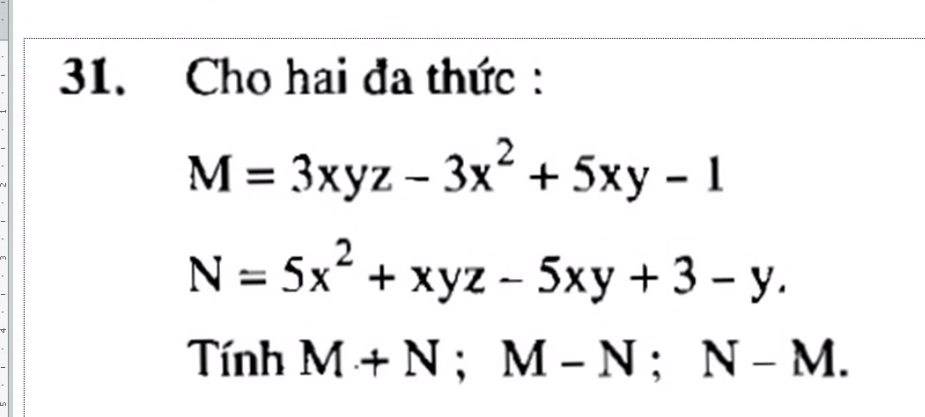
giúp em với ạ em cần gấp ạ
giúp em với ạ em cần gấp ạ
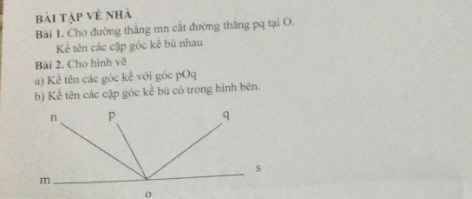
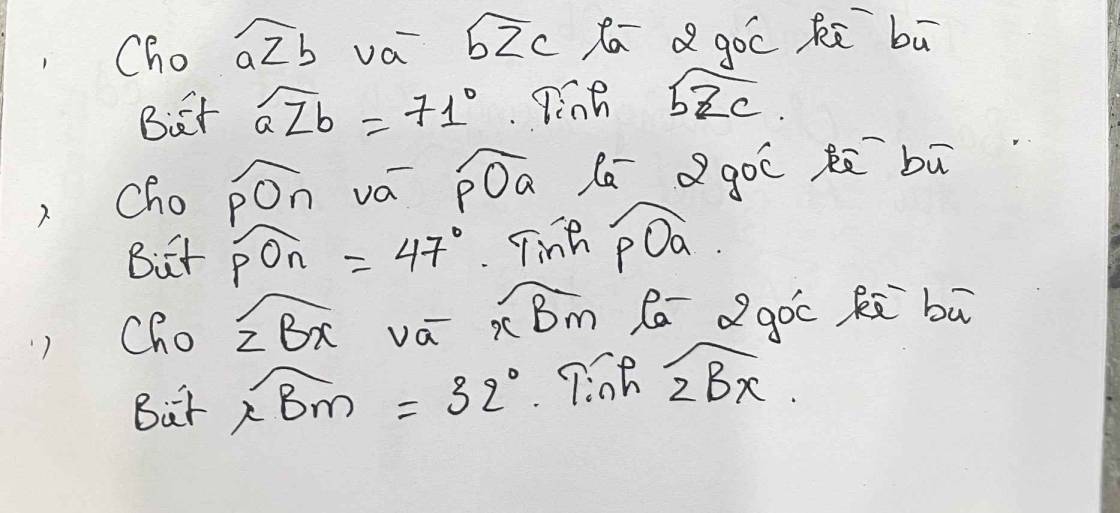GIẢI GẤP GIÚP T Ạ, T CẦN GẤP 
