Trên cùng 1 quãng đường vận tốc mỗi người tỷ lệ nghịch với thời gian đi hết quãng đường đó của mỗi người nên
Vận tốc người đi từ A / vận tốc người đi từ B = thời gian người đi từ B / thời gian người đi từ A = 9/6=3/2
Tính từ khi khởi hành đến khi gặp nhau quãng đường đi được của mỗi người tỷ lệ thuận với vận tốc của mỗi người nên
Quãng đường người đi từ A / quãng đường người đi từ B = vận tốc của người đi từ A / vận tốc người đi từ B = 3/2
Gọi quãng đường AB là S thì
Quãng đường người thứ nhất đi từ A đến chỗ gặp nhau là
\(\dfrac{Sx3}{3+2}=\dfrac{3S}{5}\)
Vận tốc của người đi từ A là
\(S:6=\dfrac{S}{6}\)
Thời gian hai người gặp nhau là
\(\dfrac{3S}{5}:\dfrac{S}{6}=\dfrac{3S}{5}x\dfrac{6}{S}=\dfrac{18}{5}\) giờ = 3 giờ 36 phút
Mỗi giờ người thứ nhất đi được số phần quãng đường là:
\(1\div6=\dfrac{1}{6}\) (quãng đường)
Mỗi giờ người thứ hai đi được số phần quãng đường là:
\(1\div9=\dfrac{1}{9}\) (quãng đường)
Mỗi giờ cả hai người đi được số phần quãng đường là:
\(\dfrac{1}{6}+\dfrac{1}{9}=\dfrac{5}{18}\) (quãng đường)
Hai xe sẽ gặp nhau sau số giờ kể từ lúc khởi hành là:
\(1\div\dfrac{5}{18}=\dfrac{18}{5}\) (giờ)










 2 bài này các bạn giúp mik phần d,e,f với
2 bài này các bạn giúp mik phần d,e,f với  còn bài này các bạn giúp mik phần c, h
còn bài này các bạn giúp mik phần c, h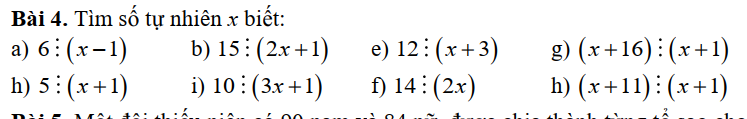 bài này các bạn giúp mik phần g, h, i
bài này các bạn giúp mik phần g, h, i các bạn giúp mik hết luôn hai bài này nhé, mik đang cần cực kì gấp
các bạn giúp mik hết luôn hai bài này nhé, mik đang cần cực kì gấp





