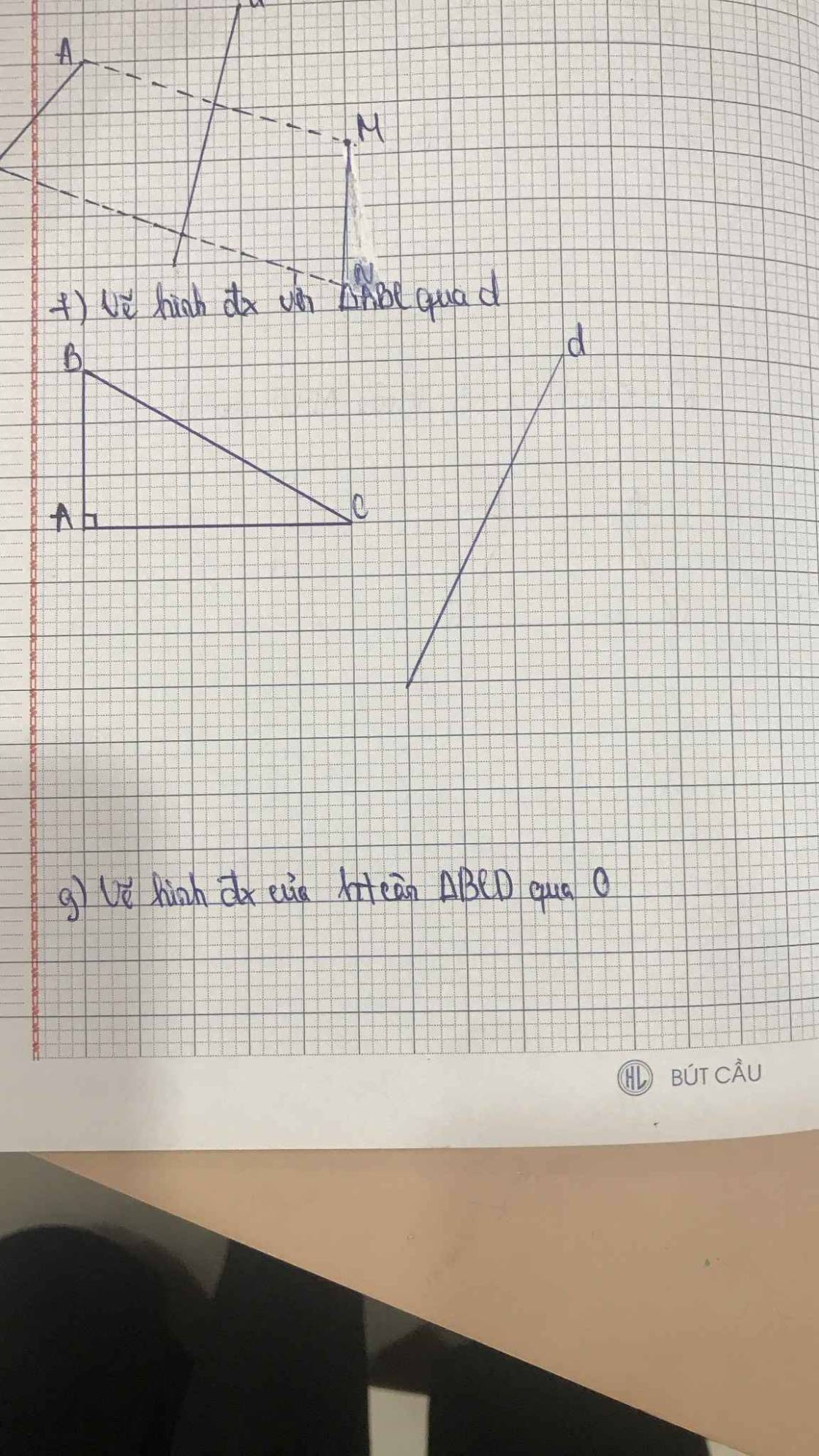
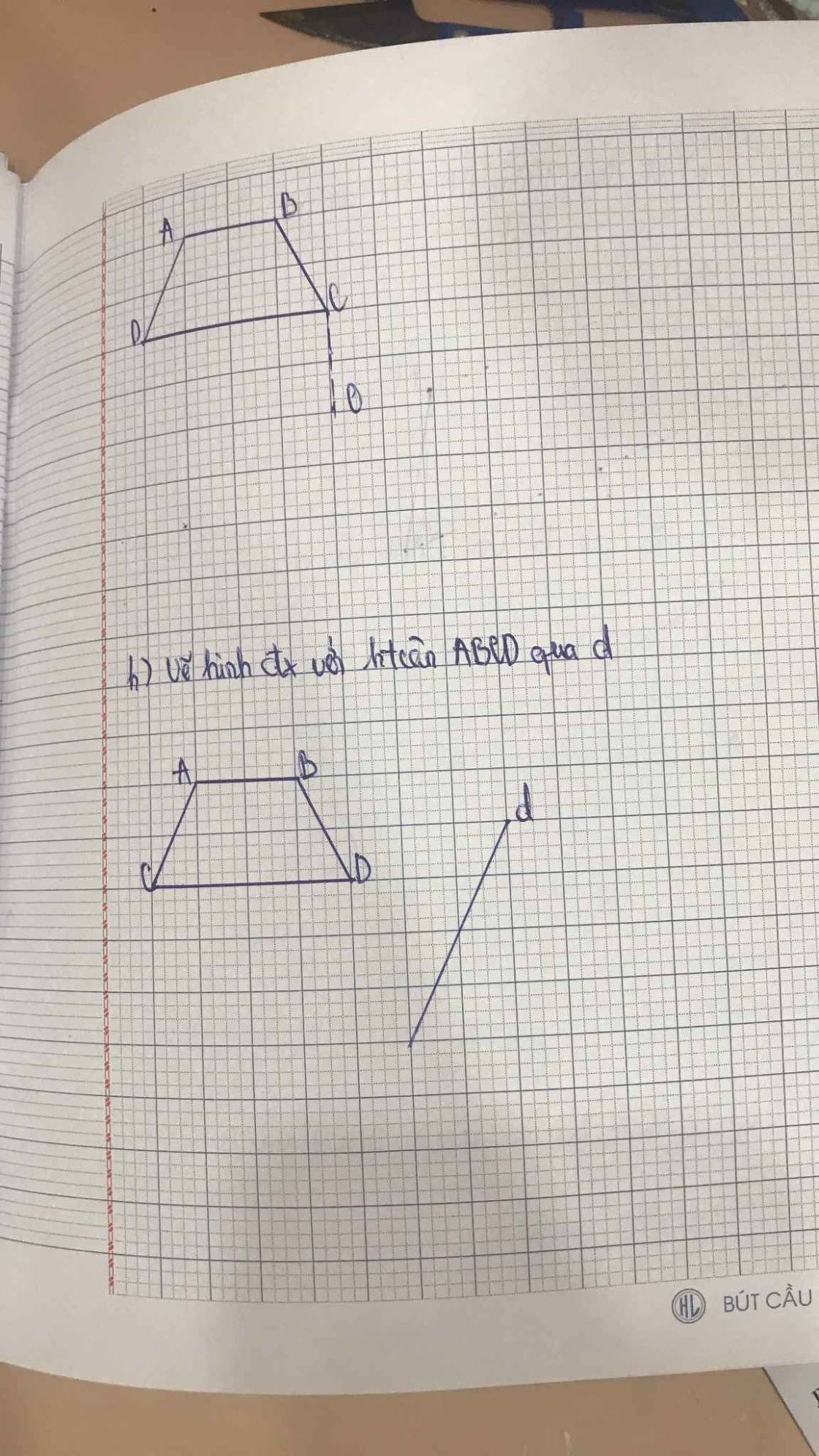
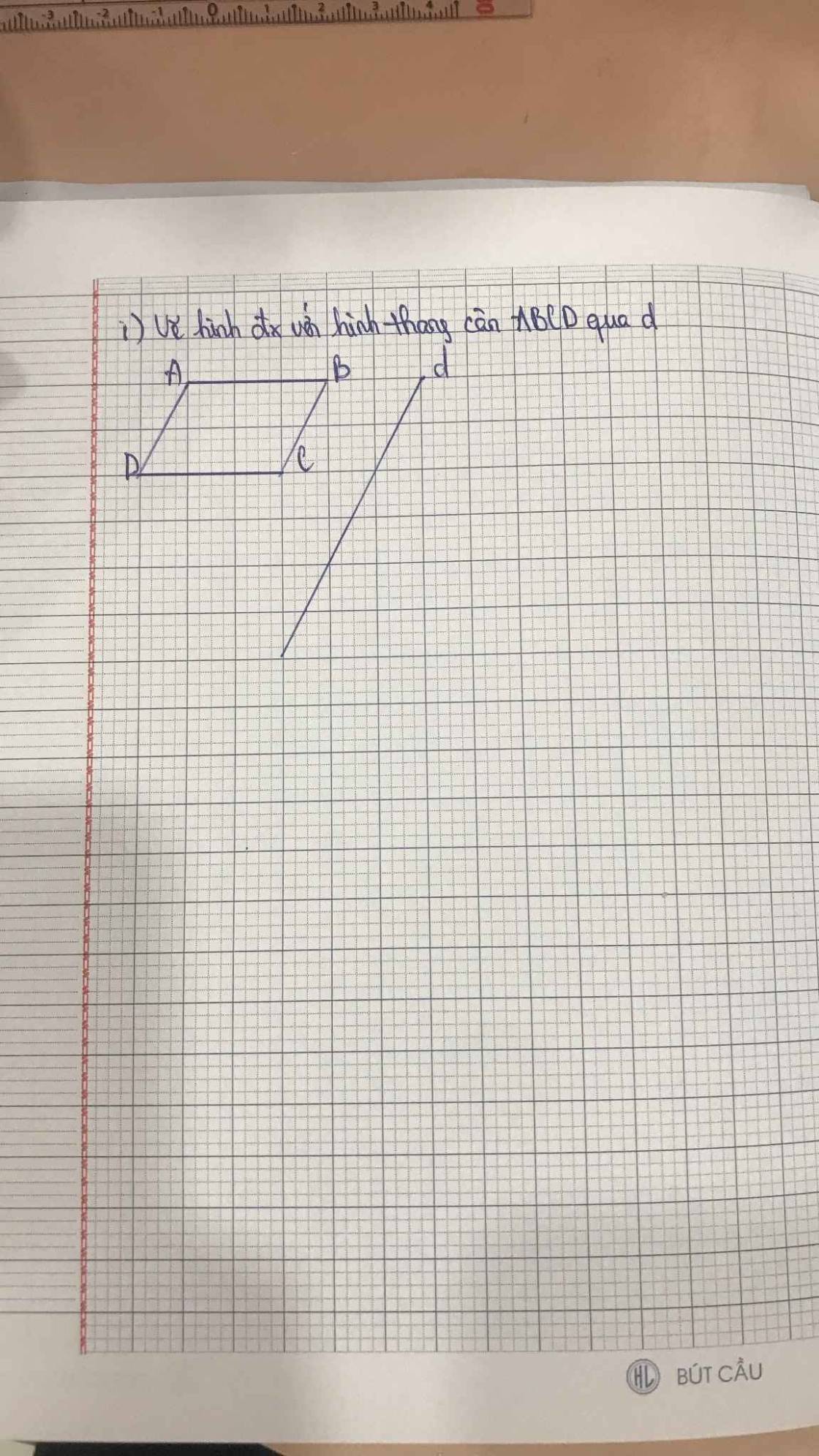
Bài 1:
a.
$5(x-3)(x-7)-(5x+1)(x-2)=25$
$\Leftrightarrow 5(x^2-10x+21)-(5x^2-9x-2)=25$
$\Leftrightarrow 5x^2-50x+105-5x^2+9x+2=25$
$\Leftrightarrow -41x+107=25$
$\Leftrightarrow 41x=82$
$\Leftrightarrow x=2$
b.
$3(x-7)(x+5)-(x-1)(3x+2)=-13$
$\Leftrightarrow 3(x^2-2x-35)-(3x^2-x-2)=-13$
$\Leftrightarrow 3x^2-6x-105-3x^2+x+2=-13$
$\Leftrightarrow -5x-103=-13$
$\Leftrightarrow -5x=90$
$x=-18$
Bài 2.
a.
$3(1-4x)(x-1)+4(3x+2)(x+3)=38$
$\Leftrightarrow 3(-4x^2+5x+1)+4(3x^2+11x+6)=38$
$\Leftrightarrow 59x+21=38$
$\Leftrightarrow 59x=17$
$\Leftrightarrow x=\frac{17}{59}
b.
$5(2x+3)(x+2)-2(5x-4)(x-1)=75$
$\Leftrightarrow 5(2x^2+7x+6)-2(5x^2-9x+4)=75$
$\Leftrightarrow 53x+22=75$
$\Leftrightarrow x=1$
c.
$2x^2+3(x-1)(x+1)=5x(x+1)$
$\Leftrightarrow 2x^2+3(x^2-1)=5x^2+5x$
$\Leftrightarrow 5x^2-3=5x^2+5x$
$\Leftrightarrow -3=5x$
$\Leftrightarrow x=-\frac{3}{5}$
d.
$(8-5x)(x+2)+4(x-2)(x+1)+2(x-2)(x+2)=0$
$\Leftrightarrow (-5x^2-2x+16)+4(x^2-x-2)+2(x^2-4)=0$
$\Leftrightarrow x^2-6x=0$
$\Leftrightarrow x(x-6)=0$
$\Rightarrow x=0$ hoặc $x=6$
Bài 3:
a.
$A=(4-5x)(3x-2)+(3-2x)(x-2)$
$=12x-8-15x^2+10x+3x-6-2x^2+4x$
$=29x-17x^2-14$
$=29.(-2)-17(-2)^2-14=-140$
b.
$B=5x(x-4y)-4y(y-5x)$
$=5x^2-20xy-4y^2+20xy$
$=5x^2-4y^2=5(\frac{-1}{5})^2-4(\frac{-1}{2})^2$
$=\frac{-4}{5}$
Bài 4.
a.
$A=x(2x+1)-x^2(x+2)+(x^3-x+3)$
$=2x^2+x-x^3-2x^2+x^3-x+3$
$=(2x^2-2x)+(x-x)+(-x^3+x^3)+3=3$ không phụ thuộc vào $x,y$ (đpcm)
b.
$B=x(x^3+2x^2-3x+2)-(x^2+2x)x^2+3x(x-1)+x-12$
$=x^4+2x^3-3x^2+2x-x^4-2x^3+3x^2-3x+x-12$
$=(x^4-x^4)+(2x^3-2x^3)+(-3x^2+3x^2)+(2x-3x+x)-12$
$=-12$ không phụ thuộc vào giá trị của $x,y$
c.
$C=3xy^2(4x^2-2y)-6y(2x^2y+1)+6(xy^3+y-3)$
$=12x^3y^2-6xy^3-12x^3y^2-6y+6xy^3+6y-18$
$=-18$ không phụ thuộc vào giá trị $x,y$ (đpcm)
d.
$D=3x(x-5y)+(y-5x)(-3y)-1-3(x^2-y^2)$
$=3x^2-15xy-3y^2+15xy-1-3x^2+3y^2$
$=(3x^2-3x^2)+(-15xy+15xy)+(-3y^2+3y^2)-1$
$=-1$ không phụ thuộc vào giá trị $x,y$ (đpcm)
Bài 5.
a.
$A=x^5(x-2020)-x^4(x-2020)+x^3(x-2020)-x^2(x-2020)+x(x-2020)-(x-2020)+1$
$=(x-2020)(x^5-x^4+x^3-x^2+x-1)+1$
$=0.(x^5-x^4+x^3-x^2+x-1)+1=1$
b.
$B=x^9(x+19)+x^8(x+19)+x^7(x+19)+...+x(x+19)+(x+19)+1$
$=(x+19)(x^9+x^8+...+x+1)+1$
$=0.(x^9+x^8+..+x+1)+1=1$
Bài 6.
a.
$2x^2(ax^2+2bx+4c)=6x^4-20x^3+8x^2$
$\Leftrightarrow 2ax^4+4bx^3+8cx^2=6x^4-20x^3+8x^2$
Đồng nhất hệ số ta có:
\(\left\{\begin{matrix} 2a=6\\ 4b=-20\\ 8c=8\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=3\\ b=-5\\ c=1\end{matrix}\right.\)
b.
$(ax+b)(x^2-cx+2)=x^3+x^2-2$
$\Leftrightarrow ax^3-acx^2+2ax+bx^2-bcx+2b=x^3+x^2-2$
$\Leftrightarrow ax^3+x^2(b-ac)+x(2a-bc)+2b=x^3+x^2-2$
Đồng nhất hệ số ta có:
\(\left\{\begin{matrix} a=1\\ b-ac=1\\ 2a-bc=0\\ 2b=-2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=1\\ b-c=1\\ 2=bc\\ b=-1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=1\\ b=-1\\ c=-2\end{matrix}\right.\)
Bài 7:
$A=(2-n)(n^2-3n+1)+n(n^2+12)+8$
$=2n^2-6n+2-n^3+3n^2-n+n^3+12n+8$
$=5n^2+5n+10=5(n^2+n+2)\vdots 5$
Ta có đpcm.
Bài 8:
$(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)$
$=[x^2-x(a+b)+ab]+[x^2-x(b+c)+bc]+[x^2-x(c+a)+ac]$
$=3x^2-2x(a+b+c)+ab+bc+ac$
$=3x^2-2x.2x+ab+bc+ac=ab+bc+ac-x^2$
Ta có đpcm.
Bài 9:
Ta có:
$(a-1)(b-1)(c-1)=(ab-a-b+1)(c-1)$
$=abc-(ab+bc+ac)+a+b+c-1$
$=0+a+b+c-1=1-1=0$
Ta có đpcm.
Bài 10:
$Q=2(x^3+y^3)-3(x^2+y^2)$
$=2[(x+y)^3-3xy(x+y)]-3[(x+y)^2-2xy]$
$=2(1-3xy)-3(1-2xy)=2-6xy-3+6xy=-1$