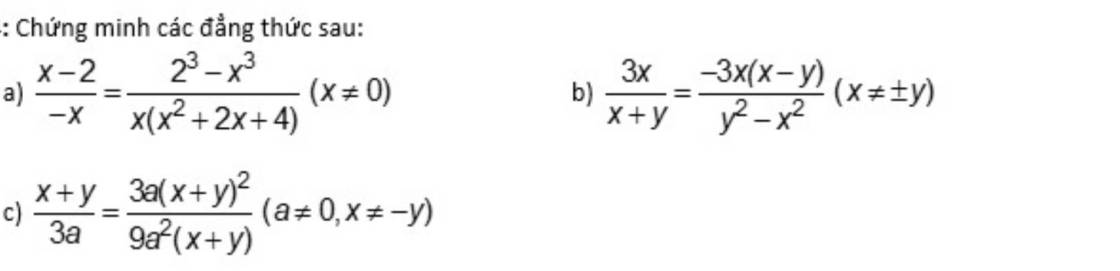a, \(\dfrac{2^3-x^3}{x\left(x^2+2x+4\right)}\) = \(\dfrac{\left(2-x\right)\left(x^2+2x+4\right)}{x\left(x^2+2x+4\right)}\) = \(\dfrac{2-x}{x}\)=\(\dfrac{x-2}{-x}\)(đpcm)
b, \(\dfrac{-3x\left(x-y\right)}{y^2-x^2}\) (\(x\) \(\ne\) \(\pm\) y)
= \(\dfrac{-3x\left(x-y\right)}{\left(y-x\right)\left(y+x\right)}\)
= \(\dfrac{3x\left(y-x\right)}{\left(y-x\right)\left(y+x\right)}\)
= \(\dfrac{3x}{x+y}\) (đpcm)
c, \(\dfrac{3a\left(x+y\right)^2}{9a^2\left(x+y\right)}\) (đk a \(\ne\)0; \(x\) \(\ne\) - y)
= \(\dfrac{3.a.\left(x+y\right)\left(x+y\right)}{3.3.a.a.\left(x+y\right)}\)
= \(\dfrac{x+y}{3a}\) (đpcm)