a) ta có :D là trung điểm của BC
mà tam giác ABC là tam giác cân
=> AD đồng thời là đường phân giác , đường cao của tam giác ABC
=> AD⊥BC
a) ta có :D là trung điểm của BC
mà tam giác ABC là tam giác cân
=> AD đồng thời là đường phân giác , đường cao của tam giác ABC
=> AD⊥BC
xét tam giác ABD vuông tại D và tam giác ACD vuông tại D có
AB = AC ( do tam giác ABC là tam giác cân)
AD chung
=> ΔABD = Δ ACD ( c.h-c.g.v)
a, Xét tg ABD và tg ACD, có:
AB=AC(tg ABC cân tại A)
AD chung.
BD=DC(D là trung điểm của cạnh BC)
=>tg ABD= tg ACD(c. c. c)
b, Vì tg ABD= tg ACD.
=>Góc BAD= góc CAD(2 góc tương ứng)
Gọi giao điểm của AD và HK là E.
Xét tg BHD và tg CKD, có:
góc K= góc H(=90o)
góc B= góc C(tg ABC cân tại A)
BD=CD(2 cạnh tương ứng)
=>tg BHD= tg CHD(ch-gn)
=>HB= KC(2 cạnh tương ứng)
Ta có: AH+HB=AB.
AK+KC=AC.
Mà AB=AC(tg ABC cân tại A), HB=HC(cmt) nên suy ra: AH=AK.
Xét tg AEH và tg AEK, có:
AH=AK(cmt)
góc AEH= Góc AEK(2 góc tương ứng)
AE chung.
=>tgAHE= tg AKE(c. g. c)
=>HE=KE(2 cạnh tương ứng)(1)
=>góc AEH= góc AEK(2 góc tương ứng)
Mà, góc AEH+ góc AEK=180o(2 góc kề bù)
=>góc AEH= góc AEK=90o.
=>AE vuông góc với HK.
=>AD vuông góc với HK(2)
Từ (1) và (2), suy ra AD là đường trung trực của HK(đpcm)
Gọi giao điểm của AD và HK là I
Vì Δ ABD= △ ACD.
==>Góc BAD= góc CAD
Xét Δ BHD và Δ CKD có:
góc K= góc H(=90o)
góc B= góc C(Δ ABC cân tại A)
BD=CD
=>Δ BHD= Δ CHD(c.h-g.n)
=>HB= KC
Ta có: AH+HB=AB.
AK+KC=AC.
Mà AB=AC(Δ ABC cân tại A)
HB=HC(cmt)
==>: AH=AK.
Xét Δ AIH và Δ AIK, có:
AH=AK(cmt)
góc AIH= Góc AIK(2 góc tương ứng)
AI chung.
=>ΔAHI= Δ AKI(c. g. c)
=>HI=KI(1)
=>góc AIH= góc AIK
Mà, góc AIH+ góc AIK=180o(2 góc kề bù)
=>góc AIH= góc AIK=90o.
=>AI vuông góc với HK.
=>AD vuông góc với HK(2)
Từ (1) và (2), suy ra: AD là đường trung trực của HK
b.Gọi giao điểm của AD và HK là E
Xét tam giác vuông BHD và tam giác vuông CKD, có:
^B = ^C ( ABC cân )
BD = CD ( gt )
Vậy tam giác vuông BHD = tam giác vuông CKD ( ch.gn )
=> BH = CK ( 2 cạnh tương ứng )
Mà AB = AC
=> AH = AK
=> Tam giác AHK cân tại A
Tam giác ABC có AD là đường trung tuyến
=> AD cũng là đường cao và đường phân giác
=> AD vuông với BC ( 1 )
=> ^BAD = ^ CAD
Tam giác AHK cân tại A, mà ^BAD = ^CAD
=> AD là đường cao của tam giác AHK
=> AD vuông với HK ( 2 )
Từ (1) và (2) => AD là trung trực của HK
















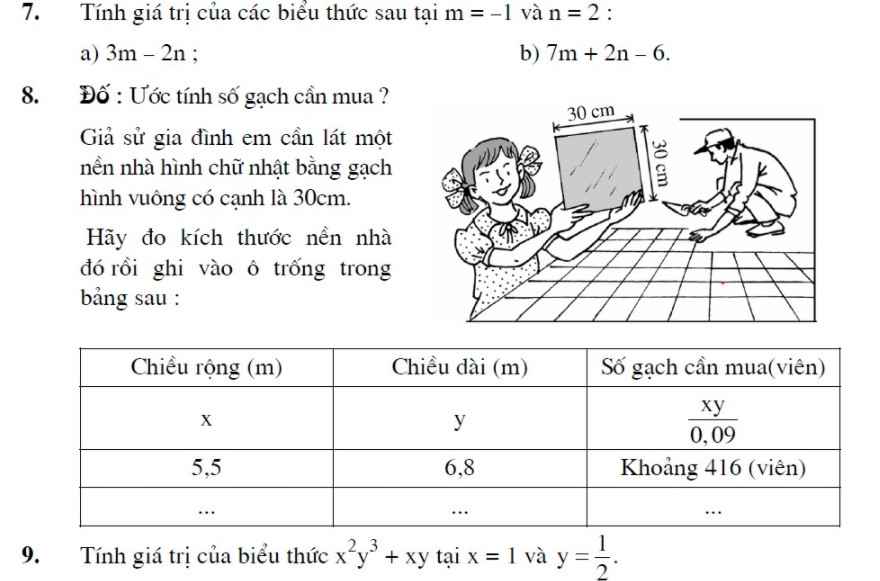 cacsbanj giúp mik vs mik gấp lắm nhơ đừng làm bài 8 nhé các bạn . mong cac bnj giupx mik
cacsbanj giúp mik vs mik gấp lắm nhơ đừng làm bài 8 nhé các bạn . mong cac bnj giupx mik

 các bạn giúp mik vs ạ , dấu bút xóa là dấu nhân nhé ! gấp ạ
các bạn giúp mik vs ạ , dấu bút xóa là dấu nhân nhé ! gấp ạ
