Các câu hỏi tương tự
Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O (n
∈
N*, n
≥
2). Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n? A. 20 B. 12 C. 15 D. 10
Đọc tiếp
Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O (n ∈ N*, n ≥ 2). Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là 3 29 . Tìm n?
A. 20
B. 12
C. 15
D. 10
Cho H là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O n ∈ N , n ≥ 2 . Gọi S là tập hợp các tam giác có ba đỉnh là các đỉnh của đa giác H . Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn được một tam giác vuông trong tập S là 1 3. Tìm n.
Cho đa giác đều A 1 A 2 A 3 . . . A 30 nội tiếp trong đường tròn (O). Tính số hình chữ nhật có các đỉnh là 4 trong 30 đỉnh của đa giác đó.
A. 105.
B. 27405.
C. 27406.
D. 106.
Chứng minh rằng trong không gian 3 chiều chỉ có đúng 5 khối đa diện đều: Tứ diện đều (3 mặt tam giác), Lập phương (3 mặt vuông), Bát diện đều (8 mặt tam giác), Thập nhị diện đều (12 mặt ngũ giác) và Nhị thập diện đều (20 mặt tam giác)Mọi người giúp mình giải câu này với ạ :)
Đọc tiếp
Chứng minh rằng trong không gian 3 chiều chỉ có đúng 5 khối đa diện đều: Tứ diện đều (3 mặt tam giác), Lập phương (3 mặt vuông), Bát diện đều (8 mặt tam giác), Thập nhị diện đều (12 mặt ngũ giác) và Nhị thập diện đều (20 mặt tam giác)

Mọi người giúp mình giải câu này với ạ :)
Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O (n ∈ N*, n ≥ 2). Gọi S là tập hợp các tam giác có ba đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn được một tam giác vuông trong tập S là 1/3. Tìm n.
Cho đa giác đều 100 đỉnh nội tiếp một đường tròn. Số tam giác tù được tạo thành từ 3 trong 100 đỉnh của đa giác là
A. 44100.
B. 78400.
C. 117600.
D. 58800.
Giúp em giải bài này với ạ! Em cảm ơn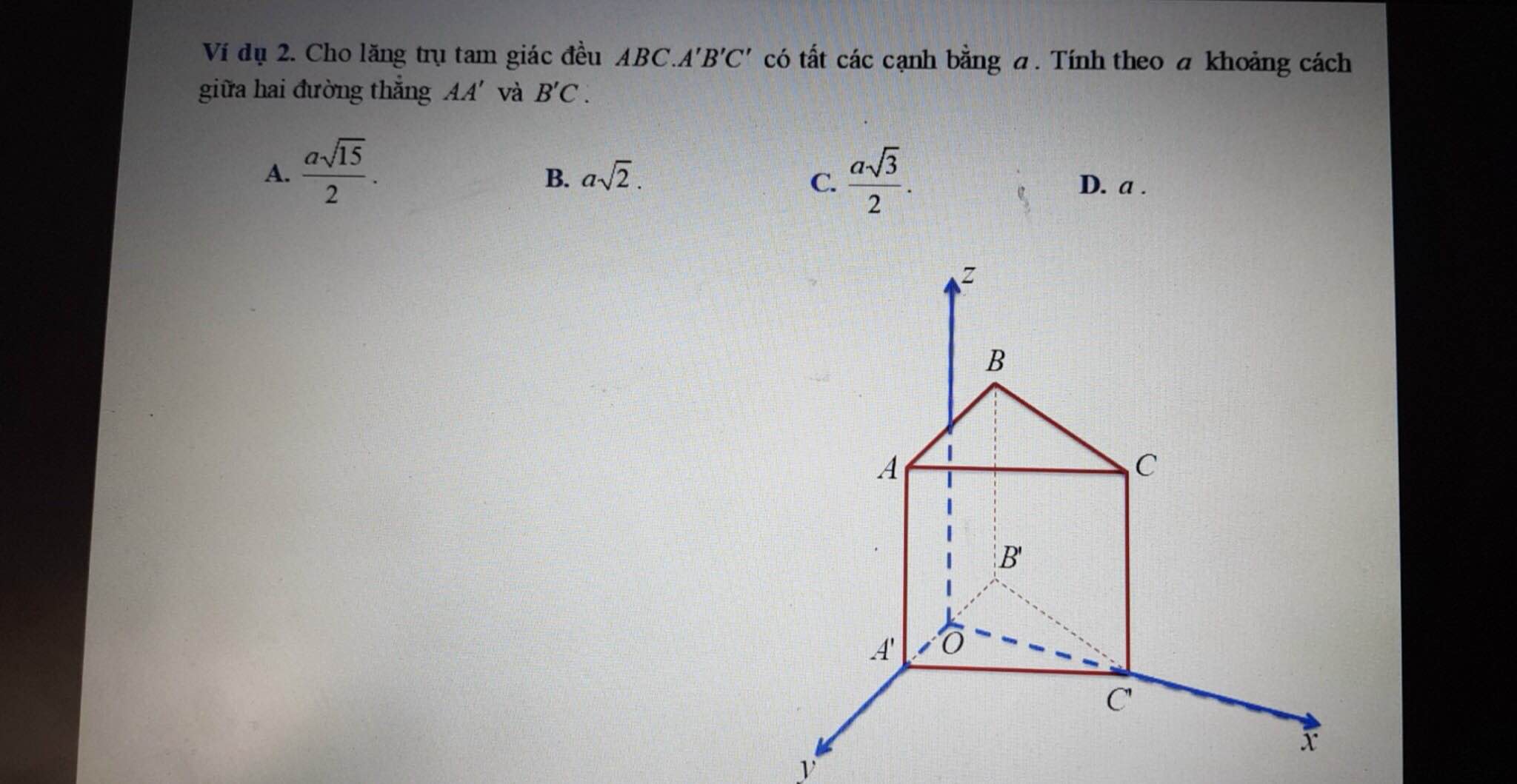
Cho lăng trụ lục giác đều ABCDEF.A'B'C'D'E'F'. O và O' là tâm đường tròn ngoại tiếp hai đáy, mặt phẳng (P) đi qua trung điểm của OO' và cắt các cạnh bên của lăng trụ. Chứng minh rằng (P) của lăng trụ đã cho thành hai đa diện có thể tích bằng nhau
Mng giúp em bài này với ạ, em xin cảm ơn !😢









