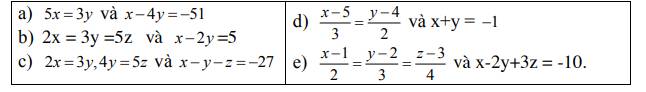`#3107.101107`
c)
Ta có:
`2x = 3y`
`=> x/3 = y/2 => x/15 = y/10`
`4y = 5z`
`=> y/5 = z/4 => y/10 = z/8`
`=> x/15 = y/10 = z/8`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/15 = y/10 = z/8 = (x - y - z)/(15 - 10 - 8) = (-27)/(-3) = 27/3 = 9`
`=> x/15 = y/10 = z/8 = 9`
`=>`\(x=15\cdot9=135\\ y=9\cdot10=90\\ z=8\cdot9=72\)
Vậy, giá trị của `x; y; z` lần lượt là `135; 90; 72`
d)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(x - 5)/3 = (y - 4)/2 = (x - 5 + y - 4)/(3 + 2) = (x + y - 5 - 4)/5 = (-1-9)/5 = (-10)/5 = -2`
`=> (x - 5)/3 = (y - 4)/2 = -2`
`=>`
\(x=\left(-2\cdot3\right)+5=-1\)
\(y=\left(-2\cdot2\right)+4=0\)
Vậy, giá trị của `x; y` lần lượt là `-1; 0`
e)
`(x - 1)/2 = (y - 2)/3 = (z - 3)/4`
`=> (x - 1)/2 = (2y - 4)/6 = (3z - 9)/12`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`(x - 1)/2 = (2y - 4)/6 = (3z - 9)/12 = (x - 1 - (2y - 4) + 3z - 9)/(2 - 6 + 12) =`\(\dfrac{x-1-2y+4+3z-9}{8}=\dfrac{x-2y+3z+\left(-1+4-9\right)}{8}\\ =\dfrac{-10-6}{8}=\dfrac{-16}{8}=-2\)
`=> (x - 1)/2 = (y - 2)/3 = (z - 3)/4 = -2`
`=>`\(x=\left(-2\cdot2\right)+1=-3\); \(y=\left(-2\cdot3\right)+2=-4\); \(z=\left(-2\cdot4\right)+3=-5\)
Vậy, giá trị của `x; y; z` lần lượt là `-3; -4; -5.`