f(2002) = 620000 (con)
g(1999) = 380000 (con)
h(2000) = 100000 (con)
Năm 2002 sản lượng của trang trại là 620 000 con vịt ; năm 1999 sản lượng là 380 000 con gà ; năm 2000 trang trại có sản lượng là 100 000 con ngan lai.
f(2002) = 620000 (con)
g(1999) = 380000 (con)
h(2000) = 100000 (con)
Năm 2002 sản lượng của trang trại là 620 000 con vịt ; năm 1999 sản lượng là 380 000 con gà ; năm 2000 trang trại có sản lượng là 100 000 con ngan lai.
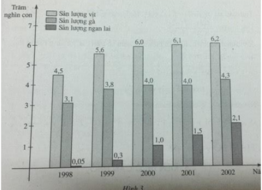
Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một trang trại. Coi y = f(x), y = g(x) và y = h(x) tương ứng là các hàm số biểu thị sự phụ thuộc số vịt, số gà và số ngan lai vào thời gian x. Qua biểu đồ, hãy:
Tìm hiệu h(2002) – h(1999) và nêu ý nghĩa của nó.
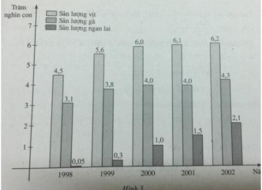
Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một trang trại. Coi y = f(x), y = g(x) và y = h(x) tương ứng là các hàm số biểu thị sự phụ thuộc số vịt, số gà và số ngan lai vào thời gian x. Qua biểu đồ, hãy:
Tìm tập xác định của mỗi hàm số đã nêu.
a. Xét dấu của biểu thức f(x) = 2x(x+2)-(x+2)(x+1)
b. Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc đồ thị của các hàm số : y = 2x(x+2) ( C1 ) và y = (x+2)(x+1)(C2)
Tính tọa độ giao điểm A và B của (C1) và (C2).
c. Tính các hệ số a, b, c để hàm số y = ax2 + bx + c có giá trị lớn nhất bằng 8 và độ thị của nó đi qua A và B.
Trên cùng một mặt phẳng tọa độ, hãy vẽ đồ thị hai hàm số y = f(x) = x + 1 và y = g(x) = 3 - x và chỉ ra các giá trị nào của x thỏa mãn:
a) f(x) = g(x);
b) f(x) > g(x);
c) f(x) < g(x).
Kiểm tra lại kết quả bằng cách giải phương trình, bất phương trình.
Cho hàm số y = f(x) có tập xác định là [−3; 3] và đồ thị của nó được biểu diễn bởi hình bên. Khẳng định nào sau đây là đúng?
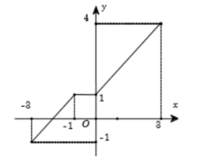
A. Hàm số đồng biến trên khoảng (−3; −1) và (1; 3).
B. Hàm số đồng biến trên khoảng (−3; −1) và (1; 4).
C. Hàm số đồng biến trên khoảng (−3; 3).
D. Hàm số nghịch biến trên khoảng (−1; 0).
Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?
A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.
B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x).
C. Số M = f( x 0 ) trong đó x 0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D
D. Nếu tồn tại x 0 ∈ D sao cho M = f( x 0 ) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.
Cho hàm số hằng y = 2
Xác định giá trị của hàm số tại x = -2; -1; 0; 1; 2.
Biểu diễn các điểm (-2;2), (-1;2), (0;2), (1;2), (2;2) trên mặt phẳng tọa độ.
Nêu nhận xét về đồ thị của hàm số y = 2.
Dựa vào đồ thị của hai hàm số đã cho trong hình 14
y = f(x) = x + 1 và y = g(x) = 1/2 x2
Hãy:
a) Tính f(-2), f(-1), f(0), f(2), g(-1), g(-2), g(0);
b) Tìm x, sao cho f(x) = 2;
Tìm x, sao cho g(x) = 2;
Cho hàm số y=f(x) = 4x^2+ 6x-5 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×). b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]