Các câu hỏi tương tự
Tìm số phức z thỏa mãn:
(
2
+
i
)
z
(
3
-
2
i
)
z
¯
-
4
(
1
-
i
)
Đọc tiếp
Tìm số phức z thỏa mãn: ( 2 + i ) z = ( 3 - 2 i ) z ¯ - 4 ( 1 - i )
![]()
![]()
![]()
![]()
Cho
z
∈
C
thỏa mãn
(
2
+
i
)
|
z
|
10
z
+
1
-
2
i
. Tìm giá trị của biểu thức T|z+1+i|+|z-(1+i)|
Đọc tiếp
Cho z ∈ C thỏa mãn ( 2 + i ) | z | = 10 z + 1 - 2 i . Tìm giá trị của biểu thức T=|z+1+i|+|z-(1+i)|
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn điều kiện
(
3
+
2
i
)
z
+
(
2
-
i
)
2
4
+
i
. Tìm phần ảo của số phức
w
(
1
+
z
)
z
¯
.
Đọc tiếp
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
![]()
![]()
![]()
![]()
Tìm phần thực a của số phức z thỏa mãn (1 + i) 2( 2 - i) z 8 + i + (1 + 2i) z. A. a 2. B. a -3. C. a -2. D. a 3.
Đọc tiếp
Tìm phần thực a của số phức z thỏa mãn (1 + i) 2( 2 - i) z = 8 + i + (1 + 2i) z.
A. a = 2.
B. a = -3.
C. a = -2.
D. a = 3.
Cho số phức z thỏa
|
z
+
2
-
i
|
|
z
¯
+
1
-
i...
Đọc tiếp
Cho số phức z thỏa | z + 2 - i | | z ¯ + 1 - i | = 2 . Tìm | z | m i n
A. | z | m i n = -3 + 10
B. | z | m i n = -3 - 10
C. | z | m i n = 3 - 10
D. | z | m i n = 3 + 10
Cho số phức z thỏa mãn
z
-
2
+
i
+
z
+
1
-
i
13
Tìm giá trị nhỏ nhất m của biểu thức
z
+
2
-
i
Đọc tiếp
Cho số phức z thỏa mãn z - 2 + i + z + 1 - i = 13 Tìm giá trị nhỏ nhất m của biểu thức z + 2 - i
![]()
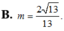

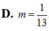
Cho số phức thỏa mãn: za+bi,
(
a
,
b
∈
R
)
thỏa mãn:
z
(
2
+
i
)
z
-
1
+
i
(
2
z
+
3
)
. Tính S a + b
Đọc tiếp
Cho số phức thỏa mãn: z=a+bi, ( a , b ∈ R ) thỏa mãn: z ( 2 + i ) = z - 1 + i ( 2 z + 3 ) . Tính S = a + b
![]()
![]()
![]()
![]()
Biết z thỏa mãn
|
z
¯
-
1
+
i
|
|
z
+
3
+
i
|
. Tìm
z
m
i
n
A.
z
m
i
n
2...
Đọc tiếp
Biết z thỏa mãn | z ¯ - 1 + i | = | z + 3 + i | . Tìm z m i n
A. z m i n = 2 5
B. z m i n = 1 5
C. z m i n = 1
D. z m i n = 3
Cho số phức z thỏa mãn (3 + 2i)z + (2 - i)2 = 4 + i. Môđun của số phức w = ( z + 1 ) z là
A. 2
B. 4
C. 10
D. 10
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7



