Các câu hỏi tương tự
Tìm các số phức 2z +
z
và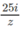 
biết rằng z = 3 – 4i
(Đề thi tốt nghiệp THPT năm 2012)
Tìm các số phức 2z + z ¯ và 25 i z biết rằng z = 3 – 4i
(Đề thi tốt nghiệp THPT năm 2012)
Biết rằng
z
-
1
2
. Tìm giá trị lớn nhất của module số phức
w
z
+
2
i
A.
5
-
2
B.
5
-
2
C.
2
+
5
D.
2
+...
Đọc tiếp
Biết rằng z - 1 = 2 . Tìm giá trị lớn nhất của module số phức w = z + 2 i
A. 5 - 2
B. 5 - 2
C. 2 + 5
D. 2 + 5
Cho số phức thỏa mãn: za+bi,
(
a
,
b
∈
R
)
thỏa mãn:
z
(
2
+
i
)
z
-
1
+
i
(
2
z
+
3
)
. Tính S a + b
Đọc tiếp
Cho số phức thỏa mãn: z=a+bi, ( a , b ∈ R ) thỏa mãn: z ( 2 + i ) = z - 1 + i ( 2 z + 3 ) . Tính S = a + b
Biết số phức z thỏa mãn đồng thời hai điều kiện
z
-
3
-
4
i
5
và biểu thức
M
|
z
+
2
|
2
-
|
z
-
i
|
2
đạt giá tri lớn nhất. Tính môđun của số phức z+i
Đọc tiếp
Biết số phức z thỏa mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = | z + 2 | 2 - | z - i | 2 đạt giá tri lớn nhất. Tính môđun của số phức z+i
Cho
|
z
-
4
+
3
i
|
3
.
Số phức z có module nhỏ nhất có phần thực bằng? A.
8
5
B.
-
6
5
C.
-
8
5
D.
6
5
Đọc tiếp
Cho | z - 4 + 3 i | = 3 . Số phức z có module nhỏ nhất có phần thực bằng?
A. 8 5
B. - 6 5
C. - 8 5
D. 6 5
Xét các số phức z a +bi thỏa mãn
z
-
3
-
2
i
2
Tính a-b biết biểu thức
S
z
+
1
-
2
i...
Đọc tiếp
Xét các số phức z = a +bi thỏa mãn z - 3 - 2 i = 2 Tính a-b biết biểu thức S = z + 1 - 2 i + 2 z - 2 - 5 i đạt giá trị nhỏ nhất.
A. - 3
B. 3
C. 4
D. 0
Biết
∫
0
1
3
x
-
1
(
x
+
3
)
2
d
x
ln
a
b
-
c
d
(
a
,
b
,...
Đọc tiếp
Biết ∫ 0 1 3 x - 1 ( x + 3 ) 2 d x = ln a b - c d ( a , b , c , d ∈ Z ) Giá trị của biểu thức a+b+c+d bằng
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn
(
x
+
3
)
2
+
(
y
-
2
)
2
+
(
z
+
1
)...
Đọc tiếp
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6