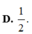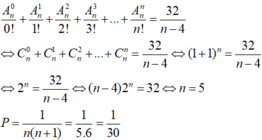Các câu hỏi tương tự
Cho các số thực a, b, c thỏa mãn
c
2
+
a
18
và
lim
x
→
+
∞
a
x
2
+
b
x
-
c
x...
Đọc tiếp
Cho các số thực a, b, c thỏa mãn c 2 + a = 18 và lim x → + ∞ a x 2 + b x - c x = - 2 . Tính P=a+b+5c.
![]()
![]()
![]()
![]()
Cho 2 điểm phân biệt A; B và 1 điểm C. Có bao nhiêu điểm D thỏa mãn A B → = C D →
A. 0
B. 1
C. 10
D. vô số
Cho hai góc nhọn a và b thỏa mãn
t
a
n
a
1
7
và
tan
b
3
4
. Tính a + b A.
π
3
B.
2
π
3
C.
π
6
D.
π
4
Đọc tiếp
Cho hai góc nhọn a và b thỏa mãn t a n a = 1 7 và tan b = 3 4 . Tính a + b
A. π 3
B. 2 π 3
C. π 6
D. π 4
Tìm số hạng chứa x5 trong khai triển \(\left(x-\dfrac{2}{x}\right)^{n^{ }}\) , biết n là số tự nhiên thỏa mãn \(C^3_n=\dfrac{4}{3}n+2C^2_n\)
A.144 B.134 C.115 D.141
Cho a, b là các số thực thuộc khoảng
0
;
π
2
và thỏa mãn điều kiện
c
o
t
a
-
tan
π
2
-
b
a
-
b
.Tính giá trị của biểu thức
P
3...
Đọc tiếp
Cho a, b là các số thực thuộc khoảng 0 ; π 2 và thỏa mãn điều kiện c o t a - tan π 2 - b = a - b .Tính giá trị của biểu thức P = 3 a + 7 b a + b
A. P=5
B. P=2
C. P=4
D. P=6
Biết
n
∈
ℤ
+
,
n
4
và thỏa mãn
A
n
0
0
!
+
A
n
1
1
!
+
A
n
2
2...
Đọc tiếp
Biết n ∈ ℤ + , n > 4 và thỏa mãn A n 0 0 ! + A n 1 1 ! + A n 2 2 ! + A n 3 3 ! + . . . + A n n n ! = 32 n - 4 Tính P = 1 n ( n + 1 )
A. 1 42
B. 1 30
C. 1 56
D. 1 72
Cho hình lăng trụ ABC.ABC có đáy là tam giác đều cạnh 3a. Hình chiếu vuông góc của C’ lên mặt phẳng (ABC) là điểm D thỏa mãn
D
C
⇀
-
2
D
B
⇀
. Góc giữa đường thẳng AC’ và mặt phẳng (ABC) bằng
45
0
. Tính theo a thể tích khối lăng trụ ABC.ABC.
A
....
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh 3a. Hình chiếu vuông góc của C’ lên mặt phẳng (ABC) là điểm D thỏa mãn D C ⇀ = - 2 D B ⇀ . Góc giữa đường thẳng AC’ và mặt phẳng (A'B'C') bằng 45 0 . Tính theo a thể tích khối lăng trụ ABC.A'B'C'.
A . 9 a 3 21 4
B . 3 a 3 21 4
C . 27 a 3 21 4
D . a 3 21 4
Cho
∆
ABC và điểm M thỏa mãn
B
M
⇀
2
C
M
⇀
. F là một phép dời hình. Gọi
A
1
F
(
A
)
,
B
1
F
(
B...
Đọc tiếp
Cho ∆ ABC và điểm M thỏa mãn B M ⇀ = 2 C M ⇀ . F là một phép dời hình. Gọi A 1 = F ( A ) , B 1 = F ( B ) , C 1 = F ( C ) , M 1 = F ( M ) . Biết AB = 4, BC = 5, AC = 6. Khi đó độ dài đoạn A 1 M 1 bằng:
A . 106
B . 138
C . 122
D . 38
Cho góc
α
thỏa mãn
π
α
3
π
2
và
sinα
-
2
cosα
1
Tính A
2
tan
α
-
c
o
t
α
Đọc tiếp
Cho góc α thỏa mãn π < α < 3 π 2 và sinα - 2 cosα = 1
Tính A= 2 tan α - c o t α
![]()
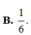
![]()