Các câu hỏi tương tự
Xét các số phức z thỏa mãn (
z
¯
+i)(z+2) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng A. 1 B.
5
4
C.
5
2
D.
3
2
Đọc tiếp
Xét các số phức z thỏa mãn ( z ¯ +i)(z+2) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả
các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng
A. 1
B. 5 4
C. 5 2
D. 3 2
Cho số phức z thỏa mãn
z
+
3
i
+
z
-
3
i
10
. Gọi
M
1
;
M
2
lần lượt là điểm biểu diễn số phức z có môđun lớn nhất và nhỏ nhất. Gọi M là trung điểm của
M
1...
Đọc tiếp
Cho số phức z thỏa mãn z + 3 i + z - 3 i = 10 . Gọi M 1 ; M 2 lần lượt là điểm biểu diễn số phức z có môđun lớn nhất và nhỏ nhất. Gọi M là trung điểm của M 1 M 2 , M(a, b) biểu diễn số phức w, tổng a + b nhận giá trị nào sau đây?
A. 7 2
B. 5
C. 4
D. 9 2
Tập hợp điểm biểu diễn số phức z thỏa mãn |z| = 1 và phần ảo của z bằng 1 là:
A. Giao điểm của đường tròn tâm O, bán kính R = 1 và đường thẳng x = 1.
B. Đường tròn tâm O, bán kính R = 1.
C. Giao điểm của đường tròn tâm O, bán kính R = 1 và đường thẳng y = 1.
D. Đường thẳng y = 1.
Cho số phức z có phần thực và phần ảo đều khác 0. Khi đó số phức z và w
-
z
¯
được biểu diễn hình học bởi 2 điểm M, N thì M và N: A. Đối xứng qua gốc O B. Đối xứng qua Oy C. Đối xứng qua Ox D. Cả A, B, C đều sai
Đọc tiếp
Cho số phức z có phần thực và phần ảo đều khác 0. Khi đó số phức z và w= - z ¯ được biểu diễn hình học bởi 2 điểm M, N thì M và N:
A. Đối xứng qua gốc O
B. Đối xứng qua Oy
C. Đối xứng qua Ox
D. Cả A, B, C đều sai
Cho số phức z có phần thực và ảo đều khác 0. Gọi M và M’ là các điểm biểu diễn các số phức (-z) và
z
¯
. Chọn khẳng định đúng. A. M
≡
M B. M,M đối xứng nhau qua Oy C. M,M đối xứng nhau qua O D. M,M đối xứng nhau qua Ox
Đọc tiếp
Cho số phức z có phần thực và ảo đều khác 0. Gọi M và M’ là các điểm biểu diễn các số phức (-z) và z ¯ . Chọn khẳng định đúng.
A. M ≡ M'
B. M,M' đối xứng nhau qua Oy
C. M,M' đối xứng nhau qua O
D. M,M' đối xứng nhau qua Ox
Trên mặt phẳng tọa độ, tìm tập hợp biểu diễn của các số phức z thỏa mãn điều kiện: Phần thực của z thuộc đoạn [-1; 2], phần ảo của z thuộc đoạn [0; 1]
Biết số phức z thỏa mãn: (2-z)
i
+
z
¯
∈
ℝ
thì tập hợp điểm biểu diễn số phức z là: A. Một đường tròn. B. Một Parabol. C. Một Elip. D. Một đường thẳng.
Đọc tiếp
Biết số phức z thỏa mãn: (2-z) i + z ¯ ∈ ℝ thì tập hợp điểm biểu diễn số phức z là:
A. Một đường tròn.
B. Một Parabol.
C. Một Elip.
D. Một đường thẳng.
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện:
a) Phần thực của z bẳng -2
b) Phần ảo của z bẳng 3
c) Phần thực của z thuộc khoảng (-1;2)
d) Phần ảo của z thuộc đoạn [1;3]
e) Phần thực và phần ảo đều thuộc đoạn [-2; 2]
Cho số phức z thỏa mãn z-4+6i-5+7i . Điểm nào sau đây trong các điểm M,N,P,Q biểu diễn cho số phức z? A.Điểm . B. Điểm . C.Điểm. D. Điểm .
Đọc tiếp
Cho số phức z thỏa mãn z-4+6i=-5+7i . Điểm nào sau đây trong các điểm M,N,P,Q biểu diễn cho số phức z?
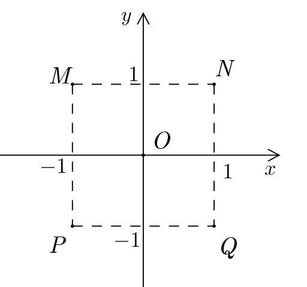
A.Điểm ![]() .
.
B. Điểm ![]() .
.
C.Điểm![]() .
.
D. Điểm ![]() .
.