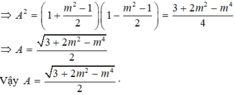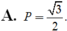Ta có (sinα + cosα ) 2 = sin 2 α + 2sinαcosα + cos 2 α = 1 + 2sinαcosα
Mặt khác sinα + cosα = m nên sinα + cosα = m ⇔ (sinα + cosα ) 2 = m 2
⇔ sin 2 α + cos 2 α + 2sinαcosα = m 2
⇔ 1 + 2sinαcosα = m 2
⇔ 2sinαcosα = m 2 - 1
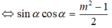
Đặt A = |sin4 α - cos 4 α |.
Ta có:
A = | sin 4 α - cos4α |
= |( sin 2 α - cos 2 α )( sin 2 α + cos 2 α )|
=|(sinα + cosα )(sinα - cosα )|

⇒ A 2 = (sinα + cosα ) 2 (sinα - cosα ) 2 = (1 + 2sinxcosx)(1 - 2sinxcosx)
⇒ A 2 = (1 + 2sinxcosx)(1 - 2sinxcosx )