Các câu hỏi tương tự
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?a) {y x + sinx, y x với 0
≤
x
≤
π
} và {y x + sinx, y x với
π
≤
x
≤
2
π
}b) {y sinx, y 0 với 0
≤
x
≤
π
} và {y cosx, y 0 với 0
≤
x
≤
π
};c) {y ...
Đọc tiếp
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π } và {y = x + sinx, y = x với π ≤ x ≤ 2 π }
b) {y = sinx, y = 0 với 0 ≤ x ≤ π } và {y = cosx, y = 0 với 0 ≤ x ≤ π };
c) {y = x , y = x 2 }
và { y = 1 - x 2 , y = 1 − x}
Biết
∫
3
4
d
x
(
x
+
1
)
(
x
-
2
)
a
ln
2
+
b
ln
5
+
c
, với a,b,c là...
Đọc tiếp
Biết ∫ 3 4 d x ( x + 1 ) ( x - 2 ) = a ln 2 + b ln 5 + c , với a,b,c là các số hữu tỉ. Tính S = a - 3b + c
A. S = 3
B. S = 2
C. S = -2
D. S = 4
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = -π/4 và x = π/4 bằng:
A. π; B. -π;
C. ln2; D. 0
Diện tích của hình phẳng được giới hạn bởi các đường: y = tanx; y = 0; x = - π /4 và x = π /4 bằng:
A. π ; B. - π ;
C. ln2; D. 0
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?a) {y x + sinx, y x với 0 ≤ x ≤ π} và {y x + sinx, y x với π ≤ x ≤ 2π}b) {y sinx, y 0 với 0 ≤ x ≤ π} và {y cosx, y 0 với 0 ≤ x ≤ π};c) {y √x, y
x
2
}và { , y 1 − x}
Đọc tiếp
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π} và {y = x + sinx, y = x với π ≤ x ≤ 2π}
b) {y = sinx, y = 0 với 0 ≤ x ≤ π} và {y = cosx, y = 0 với 0 ≤ x ≤ π};
c) {y = √x, y = x 2 }
và {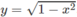 
, y = 1 − x}
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y
sin
2
/
3
x
, y 0 và x
π
/2 bằng:A. 1; B. 2/7;C. 2
π
; D. 2
π
/3.
Đọc tiếp
Thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường: y = sin 2 / 3 x , y = 0 và x = π /2 bằng:
A. 1; B. 2/7;
C. 2 π ; D. 2 π /3.
11 tháng 10 2020 lúc 10:30
(1) Cho tập hợp X={2n+1} π, với n là số nguyên. Và tập Y = {4k ±1} π, với k là số nguyên. Mối quan hệ của X và Y là:
A. X ⊂ Y
B. Y ⊂ X
C. X = Y
D. X ≠ Y
Cho hàm số f(x) xác định trên
(
-
∞
;
-
1
)
∪
(
0
;
+
∞
)
và
f
(
x
)
1
x
2
+
x
;
f
(
1
)
ln...
Đọc tiếp
Cho hàm số f(x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) và f ' ( x ) = 1 x 2 + x ; f ( 1 ) = ln 1 2 Biết ∫ 1 2 x 2 + 1 f ( x ) d x = a ln 3 + b ln 2 + c với a,b,c là các số hữu tỉ. Giá trị biểu thức a+b+c bằng
A. 27/2
B. 1/6
C. 7/6
D. -3/2
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) f(x)
(
25
-
x
2
)
trên đoạn [-4; 4]b) f(x) |
x
2
– 3x + 2| trên đoạn [-10; 10]c) f(x) 1/sinx trên đoạn [π/3; 5π/6]d) f(x) 2sinx + sin2x trên đoạn [0; 3π/2]
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]