Đáp án D
Thay z=-2+i vào phương trình ta được:
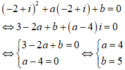
Vậy a-b=4-5=-1
Cách khác. Nghiệm liên hợp của nghiệm z 1 = - 2 + i là z 2 = - 2 - i
Ta có 
nên
z
1
,
z
2
là nghiệm của phương trình 
Do đó suy ra 
Biết phương trình z 2 + a z + b = 0 ( a , b ∈ ℝ ) có một nghiệm là z=-2+i. Tính a+b
A. 9
B. 1
C. 4
D. -1
Biết phương trình z 2 + a z + b = 0 ( a , b ∈ ℝ ) có một nghiệm là z = -2 + i. Tính a + b
A. 9.
B. 1.
C. 4
D. -1
Nghiệm phức có phần ảo dương của phương trình z 2 - z + 1 = 0 là z = a + b i , a , b ∈ ℝ . Tính a + 3 b
A. 2
B. 1
C. -2
D. -1
Biết phương trình z 2 + a z + b = 0 có một nghiệm là z = - 2 + i Tính a+b
A. 9
B. 1
C. 4
D. -1
Nếu z = i là nghiệm phức của phương trình z 2 + a z + b = 0 với a , b ∈ ℝ thì a+b bằng
A. -1.
B. 2.
C. -2.
D. 1.
Biết phương trình z 2 + a z + b = 0 ( b , c ∈ R ) có một nghiệm z=1-i. Tính môđun của số phức w=a+bi.
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(i+1) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
Cho số phức z = a + bi(a,b ∈ ℝ ) thỏa mãn z + 2 + i - |z|(1+i) = 0 và |z| > 1. Tính P = a + b
A. P = -1
B. P = -5
C. P = 3
D. P = 7
