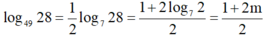Các câu hỏi tương tự
Cho
z
x
+
y
i
với x, y
∈
R
là số phức thỏa mãn điều kiện
z
¯
+
2
-
3
i
≤
|
z
+
i
-
2
|
≤
5
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ...
Đọc tiếp
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
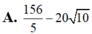
![]()
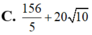
![]()
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) (x-6)
x
2
+
4
trên đoạn [0;3] có dạng a - b
c
với a là số nguyên và b, c là các số nguyên dương. Tính S a + b + c. A. 4 B. -2 C. -22 D. 5
Đọc tiếp
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) = (x-6) x 2 + 4 trên đoạn [0;3] có dạng a - b c với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b + c.
A. 4
B. -2
C. -22
D. 5
Biết rằng c và N ≠ M. Tính giá trị của MN.
A. -1
B. 1
C. 2
D. 10
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) = x 3 - 3 x 2 trên đoạn [-1;1]. Tính M + m.
A. -4
B. 4
C. -2
D. 2
Cho hai số phức z1 z2 thỏa mãn đồng thời hai điều kiện sau |z-1|=\(\sqrt{34}\) , |z+1+mi| = |z+m+2i| (trong đó m là số thực) và sao cho |z1 z2| lớn nhất.Khi đó giá trị |z1 + z2| bằng:
A:\(\sqrt{2}\)
B:10
C:2
D:\(\sqrt{130}\)
Có tất cả bao nhiêu giá trị nguyên của m để giá trị lớn nhất của hàm số
y
x
3
-
x
2
+
(
m
2
+
1
)
x
-
4
m...
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của m để giá trị lớn nhất của hàm số y = x 3 - x 2 + ( m 2 + 1 ) x - 4 m - 7 trên đoạn [ 0; 2]m không vượt quá 15 ?
A. 4
B . 6
C. 5
D. 8
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
(
S
m
)
:
(
x
-
1
)
2
+
(
y
-
1
)
2
+
(
z
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S m ) : ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - m ) 2 = m 2 4 và hai điểm A(2;3;5), B(1;2;4). Tìm giá trị nhỏ nhất của m để trên ( S m ) tồn tại điểm M sao cho M A 2 - M B 2 = 9 .
A. m=1
B. m= 3 - 3
C. m= 8 - 4 3
D. m= 4 - 3 2
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f
(
x
)
2
x
-
4
6
-
x
trên đoạn [-3;6]. Tổng M + m có giá trị là A. 18 B. -6 C. -12 D. -4
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) = 2 x - 4 6 - x trên đoạn [-3;6]. Tổng M + m có giá trị là
A. 18
B. -6
C. -12
D. -4
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên. A. 1 B. 0 C. 2 D. 4
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số ![]() có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên.
có hai điểm cực trị A, B sao cho tam giác OAB có diện tích bằng 2. Hỏi S có bao nhiêu phần tử nguyên.
A. 1
B. 0
C. 2
D. 4