Các câu hỏi tương tự
Biết hai hàm số
y
a
x
,
y
f
(
x
)
có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng
y
-
x
. Tính
f
-
a
+
f
-
a
2
A. -3 B. 4 C....
Đọc tiếp
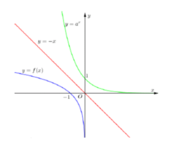
Biết hai hàm số y = a x , y = f ( x ) có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng y = - x . Tính f - a + f - a 2
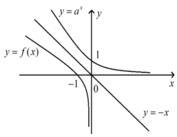
A. -3
B. 4
C. 5
D. đáp án khác
Biết đồ thị hàm số
y
log
a
x
và y f(x) đối xứng nhau qua đường thẳng y f(x)(như hình vẽ). Giá trị
f
(
-
log
a
3
)
là A. -3 B. -9 C.
-
1
3
D.
-
1
9
Đọc tiếp
Biết đồ thị hàm số y = log a x và y = f(x) đối xứng nhau qua đường thẳng y = f(x)(như hình vẽ). Giá trị f ( - log a 3 ) là
A. -3
B. -9
C. - 1 3
D. - 1 9
Biết đồ thị hàm số
y
log
a
x
và
y
f
(
x
)
đối xứng nhau qua đường thẳng
y
-
x
(như hình vẽ). Giá trị
f
-
log
a
3
là
Đọc tiếp
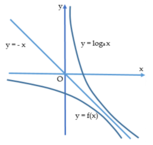
Biết đồ thị hàm số y = log a x và y = f ( x ) đối xứng nhau qua đường thẳng y = - x (như hình vẽ). Giá trị f - log a 3 là
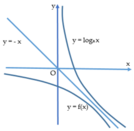
![]()
![]()
![]()
![]()
Biết đồ thị hàm số
y
log
a
x
và y f( x) đối xứng nhau qua đường thẳng y -x (như hình vẽ). Giá trị
f
(
-
log
a
3
)
là A. -3 B. -9 C.
-
1
3
D.
-
1
9
Đọc tiếp
Biết đồ thị hàm số y = log a x và y = f( x) đối xứng nhau qua đường thẳng y = -x (như hình vẽ). Giá trị f ( - log a 3 ) là
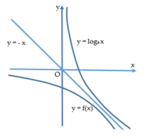
A. -3
B. -9
C. - 1 3
D. - 1 9
Cho hai hàm số y f(x) và y g(x) . Hai hàm số y f’(x) và g’(x) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y g’(x). Hàm số h(x)f(x+4)-g(2x-32) đồng biến trên khoảng nào dưới đây? A. . B. . C. . D. .
Đọc tiếp
Cho hai hàm số y= f(x) và y= g(x) . Hai hàm số y= f’(x) và g’(x) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y= g’(x).
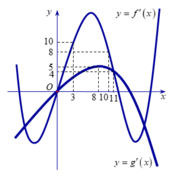
Hàm số h(x)=f(x+4)-g(2x-32) đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y f(x)
a
x
+
b
c
x
+
d
( a,b,c,d
∈
ℝ
,
-
d
c
≠
0) đồ thị hàm số y f’(x) như hình vẽ. Biết đồ thị hàm số y f(x) cắt...
Đọc tiếp
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
Cho hàm số yf( x) ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc toạ độ và đồ thị hàm số yf’( x) cho bởi hình vẽ bên. Tính f( 3) –f( 1) ? A. 24. B. 28. C. 26. D. 21.
Đọc tiếp
Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc toạ độ và đồ thị hàm số y=f’( x) cho bởi hình vẽ bên. Tính f( 3) –f( 1) ?
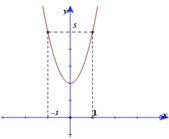
A. 24.
B. 28.
C. 26.
D. 21.
Cho hai hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
-
1
2
và
g
(
x
)
d
x
2
+
e
x
+
1
(
a
,
b
,
c
,
d...
Đọc tiếp
Cho hai hàm số f ( x ) = a x 3 + b x 2 + c x - 1 2 và g ( x ) = d x 2 + e x + 1 ( a , b , c , d , e ∈ ℝ ) . Biết rằng đồ thị của hàm số y = f(x) và y = g(x) cắt nhau tại ba điểm có hoành độ lần lượt là –3; –1;1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
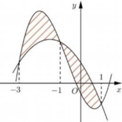
A. 9 2
B. 8
C. 4
D. 5
Cho hàm số bậc 4 y f(x) có đồ thị như hình vẽ bên. Biết hàm số y f(x) đạt cực trị tại các điểm x1,x2,x3 thỏa mãn x3 x1+2, f(x1) + f(x3) +dfrac{2}{3}f(x2) 0 và (C) nhận đường thẳng x x2 làm trục đối xứng. Gọi S1,S2,S3,S4 là diện tích của các miền hình phẳng được đánh dấu như hình bên. Tỉ số dfrac{S_1+S_2}{S_3+S_4} gần với kết quả nào nhất :
Đọc tiếp
Cho hàm số bậc 4 y = f(x) có đồ thị như hình vẽ bên. Biết hàm số y = f(x) đạt cực trị tại các điểm x1,x2,x3 thỏa mãn x3 = x1+2, f(x1) + f(x3) +\(\dfrac{2}{3}\)f(x2) = 0 và (C) nhận đường thẳng x = x2 làm trục đối xứng. Gọi S1,S2,S3,S4 là diện tích của các miền hình phẳng được đánh dấu như hình bên. Tỉ số \(\dfrac{S_1+S_2}{S_3+S_4}\) gần với kết quả nào nhất :