Đáp án là B
S = π R 2 = 64π ⇒ R = 8
Chu vi hình tròn là: C = 2πR = 2π.8 = 16π cm
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho đường tròn (O) có độ dài 20π (cm). Tính diện tích hình tròn (O).
cho hình tròn có chu vi laf15,7 cm. tính diện tích hình tròn là
Biết diện tích hình tròn là 16π. Tính chu vi của đường tròn?
A. 4 π
B. 16 π
C. 8 π
D. 12 π
Cho hình vuông ABCD có diện tích 36 cm Vuông chu vi của hình tròn ngoại tiếp hình vuông ABCD bằng
Hình bên là hình nón .chiều cao là h(cm),bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:A.
π
.
r
2
h (
c
m
3
) B. (1/3)
π
.
r
2
h (
c
m...
Đọc tiếp
Hình bên là hình nón .chiều cao là h(cm),bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:
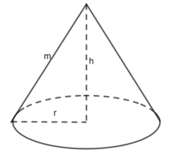
A. π . r 2 h ( c m 3 ) B. (1/3) π . r 2 h ( c m 3 )
C. π .r.m ( c m 3 ) D. π r(r+m) ( c m 3 )
Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tuyến Ax, By ( Ai, By và nửa đường tròn thuộc mặt phẳng bờ AB) . Gọi M là điểm bất kì thuộc nửa đường tròn. Tiếp tuyến M Cắt Ax , By theo thứ tự ở C, Da) Chứng minh rằng đường tròn có đường kính CD tiếp xúc với ABb) Tìm vị trí của điểm M để hình thang ABDC có chu vi nhỏ nhất c) Tìm vị trí của C , D để hình thang ABDC có chu vi bằng 14 cm, biết AB 4 cm
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tuyến Ax, By ( Ai, By và nửa đường tròn thuộc mặt phẳng bờ AB) . Gọi M là điểm bất kì thuộc nửa đường tròn. Tiếp tuyến M Cắt Ax , By theo thứ tự ở C, D
a) Chứng minh rằng đường tròn có đường kính CD tiếp xúc với AB
b) Tìm vị trí của điểm M để hình thang ABDC có chu vi nhỏ nhất
c) Tìm vị trí của C , D để hình thang ABDC có chu vi bằng 14 cm, biết AB = 4 cm
Cho đường tròn (O,R cm), điểm M nằm ngoài đường tròn cách O một khoảng 2R cm. Kẻ các tiếp tuyến MA, MB với đường tròn.
a) Chứng minh MO vuông góc với AB (đã làm)
b) Tính AB theo R
c) Tam giác ABC là tam giác gì? Tính chu vi và diện tích
d) Tia AO cắt đường tròn tại C, tứ giác CBMO là tứ giác gì? Tại sao?
Giúp mình với mình đang cần gấp
Cho đường tâm O , Mnằm ngoài đường tròn , qua M kẻ các tiếp tuyến MA , MB với đường tròn . Tia AO cắt đường tròn ở C .
a) CM : MO là trung trực của AB
b) Tứ giác BMOC là hình gì ? Vì sao ?
c) Cho R = 5 cm , AB = 8 cm . Tính chu vi tam giác MAB
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.a. tứ giác ACOD là hình jb. tam giác BCD là tam giác jc. tính chu vi và diện tích tam giác BCD3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.a. CM: tứ giác BHCD là hình...
Đọc tiếp
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với