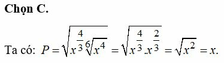Các câu hỏi tương tự
Dạng lũy thừa với số mũ hữu tỉ của biểu thức
1
8
2
5
a
x
3
7
với a 0, x 0 là:
Đọc tiếp
Dạng lũy thừa với số mũ hữu tỉ của biểu thức 1 8 2 5 a x 3 7 với a > 0, x > 0 là:
![]()
![]()
![]()
![]()
Viết dạng lũy thừa với số mũ hữu tỉ của biểu thức
1
8
2
5
a
x
3
7
a
0
,
x
0
Đọc tiếp
Viết dạng lũy thừa với số mũ hữu tỉ của biểu thức 1 8 2 5 a x 3 7 a > 0 , x > 0
![]()
![]()
![]()
![]()
Cho x là số thực dương. Biểu thức
x
2
x
3
4
được viết dưới dạng lũy thừa với số mũ hữu tỉ là: A.
x
7
12
B.
x
5
6
C.
x
12
7...
Đọc tiếp
Cho x là số thực dương. Biểu thức x 2 x 3 4 được viết dưới dạng lũy thừa với số mũ hữu tỉ là:
A. x 7 12
B. x 5 6
C. x 12 7
D. x 6 5
Chung minh rằng : , ta gọi x là số lần cân ( cân thằng bằng) , x là số tự nhiên ≥ 3 , , ta luôn tìm 1 đồng bị lỗi qua số qua số lân cân là x và số đồng tối đa là: 2.(3^x-2+ 3^x-3+3^x-4...+3^x-x) +(3^x-2+ 3^x-3^x-4...+3^x-x)+ 4-x trong đó luôn tìm được 1 đồng tiền bị lỗi . bài toán có 13 đồng tiền trong đó có 1 đồng bị lỗi không biết nặng hơn hay nhẹ hơn đồng tiền còn lại qua 3 lần cân thăng bằng tìm gia đồng bị lỗi. Lời giải:Ta đánh đấu từng đồng bằng các số từ 1 đến 13 , ta chia thành...
Đọc tiếp
Chung minh rằng : , ta gọi x là số lần cân ( cân thằng bằng) , x là số tự nhiên ≥ 3 , , ta luôn tìm 1 đồng bị lỗi qua số qua số lân cân là x và số đồng tối đa là:
2.(3^x-2+ 3^x-3+3^x-4...+3^x-x) +(3^x-2+ 3^x-3^x-4...+3^x-x)+ 4-x
trong đó luôn tìm được 1 đồng tiền bị lỗi .
 bài toán có 13 đồng tiền trong đó có 1 đồng bị lỗi không biết nặng hơn hay nhẹ hơn đồng tiền còn lại qua 3 lần cân thăng bằng tìm gia đồng bị lỗi. Lời giải:
bài toán có 13 đồng tiền trong đó có 1 đồng bị lỗi không biết nặng hơn hay nhẹ hơn đồng tiền còn lại qua 3 lần cân thăng bằng tìm gia đồng bị lỗi. Lời giải:
Ta đánh đấu từng đồng bằng các số từ 1 đến 13 , ta chia thành 3 nhóm nhóm A là nhóm có số đồng từ số 1 đến số 4 , nhóm B có số đồng từ 5 đến 8 , nhóm C có số đồng từ 9 đến 13 , lần cân thứ nhất: ta cho nhóm A cân với nhóm B nếu cân thằng bằng thì nhóm C sẽ có 1 đồng bị lỗi , ta cho đồng 12 , 13 gia ngoài, cho thêm đồng số 1 vào cùng với đồng số 9 cho lên cân vơi đồng số 11 và đồng số 10 nếu cân thăng bằng thì đồng số 1 2 và đồng số 13 có 1 đồng bị lỗi . Ta cân 1 trong 2 đồng trên vơi bất kể đồng còn lại nào thì có thể tìm gia được đồng bị lỗi, nếu cân lệnh ta gi nhớ xem nhóm nào nặng hơn , vậy là trong 3 đồng 9, 10, 11 có 1 đồng bị lỗi , lần cân thứ 3 ta cho đồng số 10 cân với đồng số 11 nếu cân thăng bằng thì đồng số 9 bị lỗi còn cân lệch thì đồng số 11 và 10 có 1 đồng bị lỗi ta lấy 2 đồng cân vơi nhau và để ý xem đồng nào cùng nặng hoặc cùng nhẹ như nhóm này ở lần cân số 2 là đồng bị lỗi.
Quay chở lại trường hợp cân nhóm A với Nhóm B nếu cân không thăng bằng ta gi nhớ xem nhóm nào nặng hơn. Ta bỏ đồng số 4 của nhóm A và đồng số 7,8 của nhóm B gia ngoài. Cho đồng số 3 sang nhóm B đồng số 6 sang nhóm A . Vậy nhóm A có đồng 1 ,2 ,6 nhóm B có đồng 3 ,5 và đồng số 9 cho thêm vào không bị lỗi. Nếu cân thăng bằng thì 3 đồng 4 ,7,8 có đồng lỗi, ta lấy đồng 7 cân với đồng 8 cũng suy luận như nhóm C là tìm đc đồng bị lỗi. Nếu cân đảo chiều thì đồng 3 hoặc đồng 6 bị lỗi, còn lần cân còn lại tìm gia được đồng nào bị lỗi. Nếu cân vẫn lệch như lần cân số 1 thì 3 đồng 1,2,5 có đồng bị lỗi ta cũng cân đồng số 1 với đồng số 2 như cách cân ở nhóm C có thể tìm gia đồng bị lỗi.
từ dữ niệu bài toán ta có :
Với 3 lần cân ta cân được tối đa 13 đồng tiền ,
Với 4 lần cân ta cân được tối đa là 39 đồng tiền ( 1 tuần trc mình nhầm to cái này) vì đơn giản là 39 đông chia thành 13 cân vơi13 , nếu thăng bằng thì 13 đồng còn lại bị lỗi và với 3 lần cân còn lại tìm đc đồng bị lỗi trong 13 đồng như là làm, còn cân lệch thì chia thành 3 nhóm 9,9,8 lấy ghép mỗi bên bên này 4 thì bên kia 5 có 3 khả năng xẩy ra ứng với 3 nhóm có số đồng là 9 hoặc 9, hoặc 8 bị lỗi , nếu 9 đồng bị lỗi thì lại chị làm 3,3,3 khác với bài toán 13 đông xu ta chia đc 3,3,2 do khi cân 2 nhóm số đồng xu cộng lại không thể lẻ đc nhầm tổng quát ở chỗ này
Với 5 lần cân thì ta được số đồng tối đa là 119 , lấy 40 đồng cân với 40 đông , cân thằng bằng thì 39 đông còn lại bị lỗi với 4 lần cân còn lại tìm đc 1 đồng bị lỗi như trên
Với 6 lần cân ta đc số đồng tối đa là 361 đồng lấy 121 cân với 121 đồng nếu cân thằng bằng thì 119 đồng còn lại bị lỗi còn cân lệch thì 242 đồng bị lỗi cho thêm 1 đồng không bị lỗi vào ta chia thành 3 nhóm mỗi nhóm có 81 đồng sắp xếp sao cho mỗi bên có 40 hoặc 41 đồng của của lần lượt 2 nhóm trên .
Với 7 lần ta có số đồng tối đa xác định đc là 364+364+361 tổng số là 1089
với 8 lần cân ta có số đồng tối đa xác định được 1 đồng bị lỗi là : 1093+1093+1089=3275
với 9 lần cân ta luôn được số đồng xu tối đa để tìm được 1 đồng xu bị lỗi là : 3280+3280+3275=9835
Tổng hợp lại bài toán với x là số lần cân x là số tự nhiên x≥ 3ta luôn có số đồng tiền tối đa xác định đc qua x lần cân là: . Thì tìm đc 1 đồng tiền bị lỗi. 2.(3^x-2+ 3^x-3+3^x-4...+3^x-x) +(3^x-2+ 3^x-3^x-4...+3^x-x)+ 4-x
1.Tính các giá trị biểu thức sau:a)510000.log52-59999.log52-...-53.log52-52.log52?b)(x2+1).4100000-(x2+1).499999,5-...-(x2+1).43.5-(x2+1).43?c)(π+e).256500000-(π+e).256499999.875-...-(π+e).2561.125-256(π+e)?d)(frac{1}{pi}.1650000-frac{1}{pi}.1649999.75-...-frac{1}{pi}.162.25-frac{1}{pi}.162).(π.4150000-π.4149999.5-...-π.44.5-π.44)?e)(x-2).(sqrt{x+1})100000-(x-2).(sqrt{x+1})99999.5-...-(x-2).(sqrt{x+1})4.5-(x-2).(sqrt{x+1})4?f)(1/x)5.(1/2)-150000-(1/x)5.(1/2)-149999-...-(1/x)5.(1/2)-6-(1/x)5.(1/2...
Đọc tiếp
1.Tính các giá trị biểu thức sau:
a)510000.log52-59999.log52-...-53.log52-52.log52=?
b)(x2+1).4100000-(x2+1).499999,5-...-(x2+1).43.5-(x2+1).43=?
c)(π+e).256500000-(π+e).256499999.875-...-(π+e).2561.125-256(π+e)=?
d)(\(\frac{1}{\pi}\).1650000-\(\frac{1}{\pi}\).1649999.75-...-\(\frac{1}{\pi}\).162.25-\(\frac{1}{\pi}\).162).(π.4150000-π.4149999.5-...-π.44.5-π.44)=?
e)(x-2).(\(\sqrt{x+1}\))100000-(x-2).(\(\sqrt{x+1}\))99999.5-...-(x-2).(\(\sqrt{x+1}\))4.5-(x-2).(\(\sqrt{x+1}\))4=?
f)(1/x)5.(1/2)-150000-(1/x)5.(1/2)-149999-...-(1/x)5.(1/2)-6-(1/x)5.(1/2)-5=?
2.Giải ptrình bậc cao sau:
a)x.(x2+y)150000-x.(x2+y)149999-...-x.(x2+y)2-x3-xy-2=0
b)xy(2y+1)50000-xy(2y+1)49999-...-xy(2y+1)2-2xy2-3=0
c)x2(x+1)10000-x2(x+1)9999-...-x2(x+1)2-x2(x+1)-x2-1=0
d)x.(\(\sqrt{x+1}\))10000-x.(\(\sqrt{x+1}\))9998-...-x.(\(\sqrt{x+1}\))4-x-3=0
e)x50000-x49998-x49996-x49994-...-x8-x6-x4-x2-2=0
f)1+x+x2+...+x49998+x49999+x50000=0
g)(-2x)500000-(-2x)499999-...-(-2x)2+2(x-1)=0
h)(2x)100000-(x2)99999.5-...-(2x)1-(x2)0.5-2=0
i)cos(-x-1)100000+sin(-x-1)99999-cos(-x-1)99998+...-cos(-x-1)2+sin(-x-1)-1=0
k)(22^x)100000-(22^x)99999.99805-...-(22^x)0.001953125-2=0
l)(e3x/8+πx/3)250000-(e3x/8+πx/3)249999-...-(e3x/8+πx/3)2-e3x/8-πx/3-2=0
3.Tính giá trị tại vị trí gián đoạn sau:
a)250000-249999-...-24-23=?Biết gián đoạn tại vị trí thứ 4
b)710000.log72-79999.log72-...-72.log72-7log72=?Biết gián đoạn tại vị trí 3->5
c)22+23+...+24999+25000=?Biết gián đoạn tại vị trí thứ 350 và vị trí 600
4.Thực hiện các yêu cầu sau:
Cho pt M: x.(x+1)50000-x.(x+1)49999-...-x.(x+1)3-x.(x+1)2-n=0
a.Xác định x=?
b.Tính n=?
c.Số nào dưới đây là số nguyên tố:
A.n+1/n-1
B.n+2/n-2
C.n+3/n-3
D.n+4/n-4
d.Xác định phương trình đồng dạng bậc 20(¶20)?
5.Cho ptrình bậc 2 sau:x2-2x=0
a.Xác định hàm P=?
A.P=(x-1)2(x^2-2x) B.P=(x2-2x)/(x2-2x) C.P=2xx^2 D.(x2-2x)x^2-2x
b.Xác định hàm P(x)?Biết Q(x)=2x+1
A.P(x)=2x B.P(x)=2.(x+1) C.P(x)=2.(x+2) D.P(x)=2.(x+3)
c.Tính lim(P/Q(x))=?
A.0 B.1 C.2 D.3
d.Ptrình bậc cao:250000-249999-...-22-21 ~ vs hàm nào cuả pt bậc 2?
A.2P=2(x-1)x^2-2x B.2P=2.x2.2x C.2P=2.22x D.2P=2.42x
e.Đồ thị hàm bậc cao nằm trên:
A.Trục tung B.Trục hoành C.A,B đúng D.A,C sai
f.Khi nào P=P(x)?
A.Q(x)=0 B.P(x)=0 C.P=0 D.Q(x)=P
g.Hãy biến ptrình bậc 3 sau về ptrình bậc cao:x3-x=0?
A.(x3-x)50000-(x3-x)49999-...-(x3-x)2-x3-x=0
B.(x3-x)50000-(x3-x)49999-...-(x3-x)2-x3+x=0
C.(x3+x)50000-(x3+x)49999-...-(x3+x)2-x3-x=0
D.(x3+x)50000-(x3+x)49999-...-(x3+x)2-x3+x=0
h.Từ ptrình bậc 3 ở câu g so sánh P1=(x+e)x^3-x và P2=(x+e)3.(x^3-x)
A.P1>P2 B.P1=P2 C.P1<P2 D.P1~P2
i.Từ câu h,hãy tính giá trị biểu thức sin(P1-1)+cos(P2-1)+tan(P1P2-P1-P2+1)=?
A.-3 B.-1 C.1 D.3
6.Khai triển luỹ thừa bậc cao sau sang hàm bậc cao: 42949672961000000000?
7.Giải hệ ptrình:
Cho \(\alpha\)=\(\delta\)=25650000-25649999.875-...-2560.125-1
\(\beta\)=\(\mu\)=4100000-499999.5-...-4-40.5
\(\xi\)=\(\sigma\)=16500000-16499999.75-...-160.75-160.5
\(\hept{\begin{cases}\alpha\chi+\beta\gamma=\xi\\\sigma\chi+\mu\gamma=\delta\end{cases}}\)
8.Trả lời câu hỏi sau:
a.Công thức tìm cơ số tiêu chuẩn cuả hàm bậc cao là:
A.22^x B.44^x C.1616^x D.256256^x
b.Độ biến thiên theo cơ số tiêu chuẩn cuả hàm bậc cao là:
A.1/2x B.1/4x C.1/16x D.1/256x
c.Cho cơ số a=1,157920892.1077 ứng với độ biến thiên nào sau đây:
A.1/16 B.1/256 C.1/65536 D.1/16777216
d.Cho độ biến thiên ∆=1/250000 ứng vs cơ số tiêu chuẩn nào sau đây:
A.22^50000 B.44^25000 C.1616^12500 D.256256^6250
e.Giá trị cuả hằng số trực chuẩn là:
A.0 B.1 C.2 D.3
f.Miền trực chuẩn bất định ¢(a,∆)(a khác 0,1,2) được tính theo cthức nào sau đây:
A.¢(a,∆)=a.∆x B.¢(a,∆)=a.∆1/x C.¢(a,∆)=1/a.∆x D.¢(a,∆)=1/a.∆1/x
g.Miền trực chuẩn bất định ¢(a,∆)(a khác 0,1,2) luôn dần về:
A.0 B.1 C.2 D.3
h.Miền trực chuẩn cố định ¢(a,∆)(a=0;a=1;a=2) luôn dần về:
A.a B.∆ C.0 D.1
i.Một phương trình bậc cao có nghiệm khi và chỉ khi:
A.Có cùng cơ số ứng với độ biến thiên,có cùng hệ số,miền trực chuẩn luôn dần về một giá trị cố định không thay đổi,không có tính đồng dạng
B.Có cùng cơ số ứng với độ biến thiên,có cùng hệ số,miền trực chuẩn luôn dần về giá trị cố định không thay đổi,có tính đồng dạng
C.Có cùng cơ số ứng với độ biến thiên bất kì,các hệ số bất kì,miền trực chuẩn luôn dần về giá trị cố định không thay đổi,có tính đồng dạng
D.Có cùng cơ số ứng với độ biến thiên bất kì,các hệ số bất kì,miền trực chuẩn luôn dần về giá trị xác định không thay đổi,không có tính đồng dạng
k.Giá trị biên dưới cuả miền trực chuẩn ¢(65536;1/16) để giá trị đạt giá trị đạt hằng số trực chuẩn tuyệt đối:
A.3 B.33 C.83 D.163
(Chú ý tuyệt đối=0,tương đối~0)
l.Xét ptrình sau:5.(x+y)50000-6.(x+y)49999-3.(x+y)49998-...-2(x+y)2-4.(x+y)-2=0
A.Ptrình vô nghiệm B.Ptrình vô số nghiệm C.Phương trình có 1 nghiệm D.Ptrình 50000 nghiệm phân biệt
Giúp mik với!!!
trong các hàm số sau hàm số nào đồng biến trên R: A. y= 2x-1/x+2 B. y= -x^3+x^2-5x C. y= x^3+2x+1 D.-x^4-2x^2+3
Xét sự đồng biến, nghịch biến của hàm số:
a) y = 4 + 3x – x^2
b) y = x^4 - 2x^2 + 3
c) y = -x^3 + x^2 – 5
Cho a 0. Hãy viết biểu thức
a
4
a
5
4
a
a
3
dưới dạng lũy thừa với số mũ hữu tỉ? A.
a
9
2
B.
a
19
4
C....
Đọc tiếp
Cho a > 0. Hãy viết biểu thức a 4 a 5 4 a a 3 dưới dạng lũy thừa với số mũ hữu tỉ?
A. a 9 2
B. a 19 4
C. a 23 4
D. a 3 4
Số giao điểm của đồ thị hàm số y = (x − 3)( x 2 + x + 4) với trục hoành là:
A. 2; B. 3;
C. 0; D. 1.