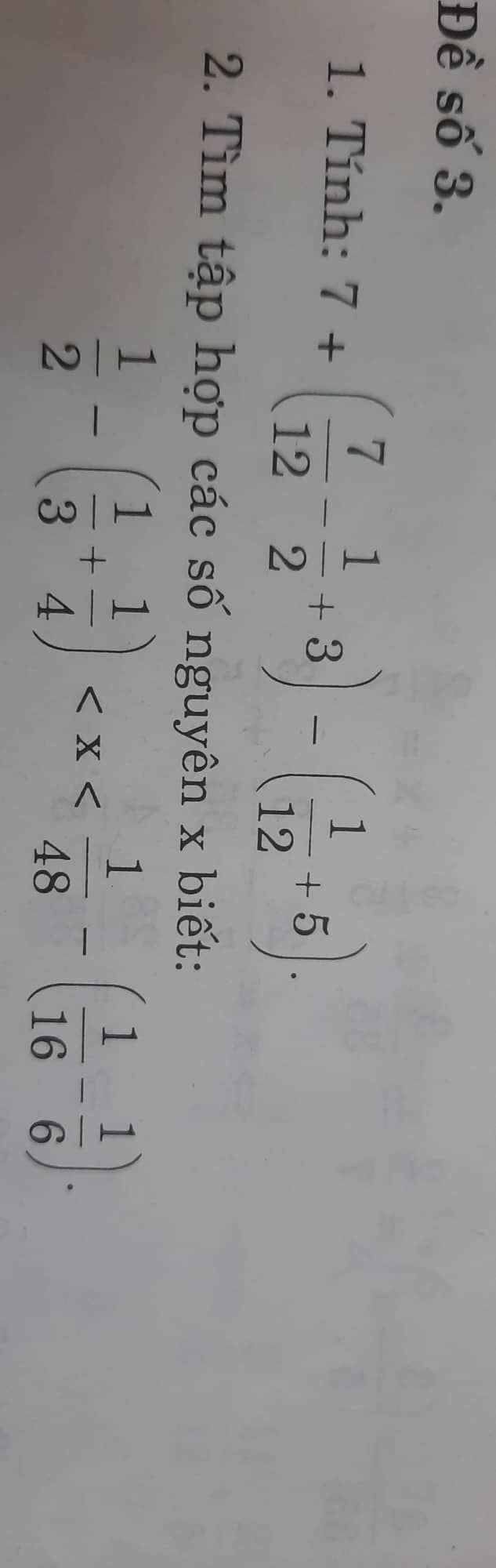Đề 3 - Bài 1
\(7+\dfrac{7}{12}-\dfrac{1}{2}+3-\dfrac{1}{12}-5=\dfrac{7}{12}-\dfrac{1}{12}+7+3-5-\dfrac{1}{2}\)
\(=\dfrac{6}{12}+5-\dfrac{1}{2}=\dfrac{1}{2}-\dfrac{1}{2}+5=5\)
Bài 2
Ta có
\(\dfrac{1}{2}-\left(\dfrac{1}{3}+\dfrac{1}{4}\right)=\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{4}=\dfrac{6-4-3}{12}=\dfrac{-1}{12}\)
\(\dfrac{1}{48}-\left(\dfrac{1}{16}-\dfrac{1}{6}\right)=\dfrac{1}{48}-\dfrac{1}{16}+\dfrac{1}{6}=\dfrac{1-3+8}{48}=\dfrac{1}{8}\)
Vậy \(\dfrac{-1}{12}< x< \dfrac{1}{8}\) (vì \(x\in Z=>x=0\))
Đề 4 - Bài 1
a) \(\dfrac{17}{6}-\left(x-\dfrac{7}{6}\right)=\dfrac{7}{4}=>\dfrac{17}{6}-x+\dfrac{7}{6}=\dfrac{7}{4}\)
\(=>-x=\dfrac{7}{4}-\dfrac{17}{6}-\dfrac{7}{6}=>-x=\dfrac{-54}{24}=>x=\dfrac{9}{4}\)
b) \(\dfrac{3}{35}-\left(\dfrac{3}{5}-x\right)=\dfrac{2}{7}=>\dfrac{3}{35}-\dfrac{3}{5}+x=\dfrac{2}{7}\)
\(=>x=\dfrac{2}{7}-\dfrac{3}{35}+\dfrac{3}{5}=>x=\dfrac{28}{35}=>x=\dfrac{4}{5}\)
Bài 2
Ta có
\(\dfrac{3}{4}-\dfrac{5}{6}=\dfrac{-1}{12}\)
\(1-\left(\dfrac{2}{3}-\dfrac{1}{4}\right)=1-\dfrac{2}{3}+\dfrac{1}{4}=\dfrac{7}{12}\)
Vậy \(\dfrac{-1}{12}\le\dfrac{x}{12}< \dfrac{7}{12}\)
Vì \(x\in Z=>x\in\left\{-1;0;1;2;3;4;5;6\right\}\)
\(7+(\dfrac{7}{12}-\dfrac{1}{2}+3)-(\dfrac{1}{12}+5)\)
\(=7+(\dfrac{7}{12}-\dfrac{6}{12}+\dfrac{1}{12})+3+5\)
\(=7+3+5 +\dfrac{1}{6}\)
\(=15+\dfrac{1}{6}=\dfrac{90}{6}+\dfrac{1}{6}=\dfrac{91}{6}\)
4.
\(a)\dfrac{17}{6}-(x-\dfrac{7}{6})=\dfrac{7}{4}\)
\(x-\dfrac{7}{6}=\dfrac{7}{4}-\dfrac{17}{6}\)
\(x-\dfrac{7}{6}=\dfrac{55}{12}\)
\(x=\dfrac{55}{12}-\dfrac{7}{6}\)
\(x=\dfrac{41}{12}\)
\(b)\dfrac{3}{35}-(\dfrac{3}{5}-x)=\dfrac{2}{7}\)
\(\dfrac{3}{5}-x=\dfrac{2}{7}-\dfrac{3}{35}\)
\(\dfrac{3}{5}-x=\dfrac{1}{5}\)
\(x=\dfrac{1}{5}-\dfrac{3}{5}\)
\(x=\dfrac{-2}{5}\)