\(2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}\)
\(2A-A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{2022}}=1-\dfrac{1}{2^{2022}}=\dfrac{2^{2022}-1}{2^{2022}}\)
\(\Rightarrow2A=1+\dfrac{1}{2}+....+\dfrac{1}{2^{2021}}\)
\(\Rightarrow2A-A=1+\dfrac{1}{2}+....+\dfrac{1}{2^{2021}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{2022}}\)
\(\Rightarrow A=1-\dfrac{1}{2^{2022}}\)

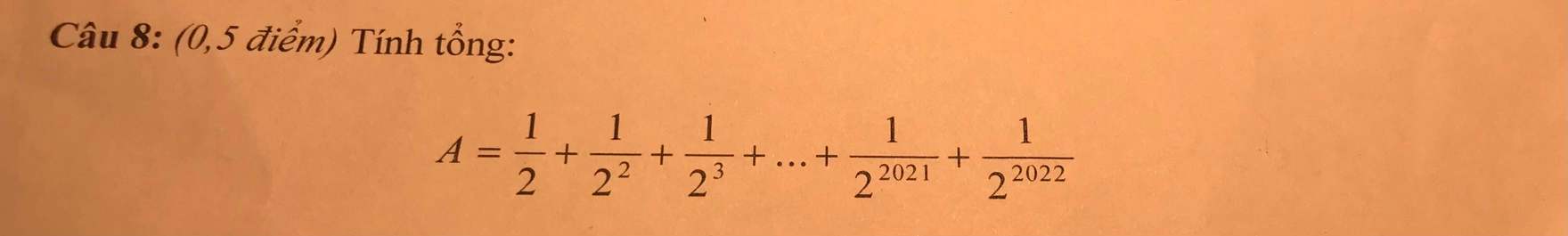 bài khó quá bạn nào là được thì giúp mình
bài khó quá bạn nào là được thì giúp mình 












