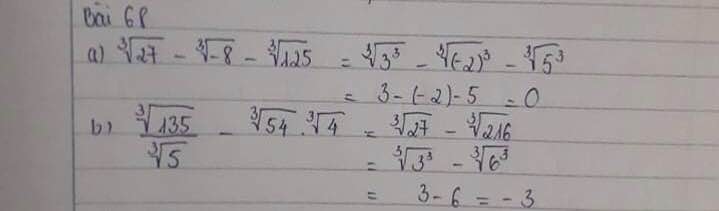Question

Bài 68 (trang 36 SGK Toán 9 Tập 1)

Tính

a) $\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}$ ;                  b) $\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54} \cdot \sqrt[3]{4}$.

Answer 1

LG a

3√27−3√−8−3√125273−−83−1253

Phương pháp giải:

Tính từng căn bậc ba rồi thực hiện phép tính

Lời giải chi tiết:

3√27−3√−8−3√125=3√33−3√(−2)3−3√53273−−83−1253=333−(−2)33−533

=3−(−2)−5=3−(−2)−5

=3+2−5=0=3+2−5=0.

LG b

 3√1353√5−3√54.3√4135353−543.43

Phương pháp giải:

Sử dụng các công thức:

3√a.b=3√a.3√ba.b3=a3.b3.

3√ab=3√a3√bab3=a3b3,  với b≠0b≠0.

Lời giải chi tiết:

3√1353√5−3√54.3√4=3√27.53√5−3√54.4135353−543.43=27.5353−54.43

=3√5.3√273√5−3√216=53.27353−2163

=3√27−3√216=273−2163

=3√33−3√63=333−633

=3−6=−3=3−6=−3.

Answer 2

a) \sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=3-(-2)-5=0327​−3−8​−3125​=3−(−2)−5=0.

b) \dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54} \cdot \sqrt[3]{4}=\sqrt[3]{\dfrac{135}{5}}-\sqrt[3]{54.4}=3-6=-335​3135​​−354​⋅34​=35135​​−354.4​=3−6=−3.

Answer 3

a) \sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=3-(-2)-5=0327​−3−8​−3125​=3−(−2)−5=0.

b) \dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54} \cdot \sqrt[3]{4}=\sqrt[3]{\dfrac{135}{5}}-\sqrt[3]{54.4}=3-6=-335​3135​​−354​⋅34​=35135​​−354.4​=3−6=−3.

Answer 4

a) \(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=3+2-5=0\)

b) \(\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}=\sqrt[3]{27}-\sqrt[3]{216}=3-6=-3\)

Answer 5

a) \sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=3-(-2)-5=0327​−3−8​−3125​=3−(−2)−5=0.

b) \dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54} \cdot \sqrt[3]{4}=\sqrt[3]{\dfrac{135}{5}}-\sqrt[3]{54.4}=3-6=-335​3135​​−354​⋅34​=35135​​−354.4​=3−6=−3

 

Answer 6

Answer 7

a/  ∛27 - ∛-8 - ∛125 = ∛33 - ∛(-2)3 - ∛53

= 3 - (-2) - 5 = 3 + 2 - 5 = 0

b/ √

135353−543.43=27.5353−54.43

53.27353−2163

$=\sqrt[3]{327}-\sqrt[3]{3216}$

$=\sqrt[3]{33^3}-\sqrt[3]{36^3}$

$=3-6=-3$

Answer 8

\(a,\\\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}\\ =3-\left(-2\right)-5\\ =3+2-5\\ =0\)

\(b,\\ \dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}\\ =\sqrt[3]{27}-\sqrt[3]{216}\\ =3-6\\ =-3\)

Answer 9

a) \(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=\sqrt[3]{3^3}-\sqrt[3]{\left(-2\right)^3}-\sqrt[3]{5^3}\)

\(=3-\left(-2\right)-5=3+2-5=0\)

b) \(\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}\cdot\sqrt[3]{4}\)

\(=\sqrt[3]{\dfrac{135}{5}}-\sqrt[3]{54\cdot4}\)

\(=\sqrt[3]{27}-\sqrt[3]{216}\)

\(=\sqrt[3]{3^3}-\sqrt[3]{6^3}=3-6=-3\)

 

Answer 10

\(a,\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}\) \(=\sqrt[3]{3^3}-\sqrt[3]{\left(-2\right)^3}-\sqrt[3]{5^3}=3+2-5=0\)

\(b,\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}\) \(=\sqrt[3]{\dfrac{135}{5}}-\sqrt[3]{54.4}=\sqrt[3]{27}-\sqrt[3]{216}\) \(=\sqrt[3]{3^3}-\sqrt[3]{6^3}=3-6=-3\)

Answer 11

\(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=3-\left(-2\right)-5=0\)

\(\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}\cdot\sqrt[3]{4}=\sqrt[3]{\dfrac{125}{5}}-\sqrt[3]{54\cdot4}=3-6=-3\)

Answer 12

a) \(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[5]{125}\)

\(=\sqrt[3]{3^3}-\sqrt[3]{\left(-2\right)^3}-\sqrt[3]{5^3}\)

\(=3-\left(-2\right)-5\)

= 0

b) \(\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}\)

\(=\sqrt[3]{\dfrac{135}{5}}-\sqrt[3]{54.4}\)

\(=\sqrt[3]{27}-\sqrt[3]{216}\)

\(=\sqrt[3]{3^3}-\sqrt[3]{6^3}\)

\(=3-6\)

= -3

Answer 13

a/=3-(-2)-5=3+2-5=0

b/3-6=-3

Answer 14

\(a.\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=\sqrt[3]{3^3}-\sqrt[3]{-2^3}-\sqrt[3]{5^3}=3-\left(-2\right)-5=0\)

\(b.\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}=\sqrt[3]{\dfrac{135}{5}}-\sqrt[3]{54.4}=\sqrt[3]{27}-\sqrt[3]{216}=\sqrt[3]{3^3}-\sqrt[3]{6^3}=3-6=-3\)

Answer 15

a)3-(-2)-5=0

b)-3

Answer 16

a,0   b,-3

Answer 17

\(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=3-\left(-2\right)-5=0\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}=\sqrt[3]{\dfrac{135}{5}}-\sqrt[3]{54.4}=3-6=-3\)

Answer 18

0;-3

Answer 19

 

Answer 20

a) a) 

\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=3-(-2)-5=0327​−3−8​−3125​=3−(−2)−5=0.

b) \dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54} \cdot \sqrt[3]{4}=\sqrt[3]{\dfrac{135}{5}}-\sqrt[3]{54.4}=3-6=-335​3135​​−354​⋅34​=35135​​−354.4​=3−6=−3.

Answer 21

a)\(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=\sqrt[3]{3^3}-\sqrt[3]{\left(-2\right)^3}-\sqrt[3]{5^3}=3-\left(-2\right)-5=3+2-5=0\)

b)\(\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}=\dfrac{\sqrt[3]{27.5}}{\sqrt[3]{5}}-\sqrt[3]{54.4}=\dfrac{\sqrt[3]{27}.\sqrt[3]{5}}{\sqrt[3]{5}}-\sqrt[3]{216}=\sqrt[3]{27}-\sqrt[3]{216}=\sqrt[3]{3}-\sqrt[3]{6}=3-6=-3\)

Answer 22

a)0

b)-3

Answer 23

Câu A bằng 0 Câu B bằng 3

Answer 24

\(a,\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=3-\left(-2\right)-5=5-5=0\)

\(b,\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}=\sqrt[3]{\dfrac{135}{5}}-\sqrt[3]{54.4}=\sqrt[3]{27}-\sqrt[3]{216}=3-6=-3\)

Answer 25

\(a\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=\sqrt[3]{\left(3\right)^3}-\sqrt[3]{\left(-2\right)^2}-\sqrt[3]{\left(5\right)^{ }3}=3-\left(-2\right)-5=0\)

b\(\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}=\sqrt[3]{\dfrac{135}{5}}-\sqrt[3]{54.4}=\sqrt[3]{27}-\sqrt[3]{216}=3-6=-3\)

Answer 26

a) kết quả = 0 
b)kết quả = -3

Answer 27

 

Answer 28

a) 0                                                b)-3

Answer 29

\(b)\dfrac{\sqrt[3]{135}}{\sqrt[3]{5}}-\sqrt[3]{54}.\sqrt[3]{4}=\sqrt[3]{27}-\sqrt[3]{27}.\sqrt[3]{8}=3-3.2=-3\) \(\sqrt[3]{27}-\sqrt[3]{-8}-\sqrt[3]{125}=\sqrt[3]{3^3-2-\sqrt[3]{5^3}=3-2-5=0}\)

Answer 30

a)=3-(-2)-5=0   ;   b)=3-6=-3