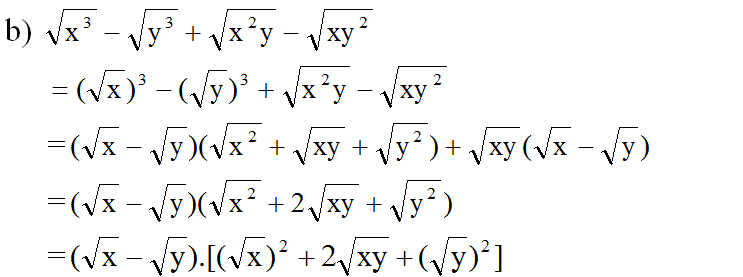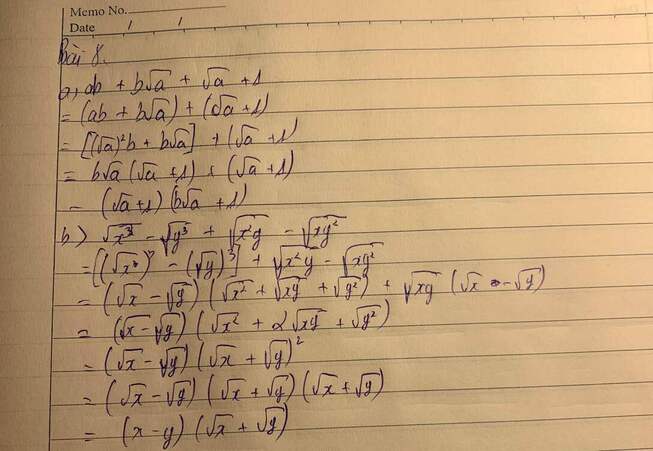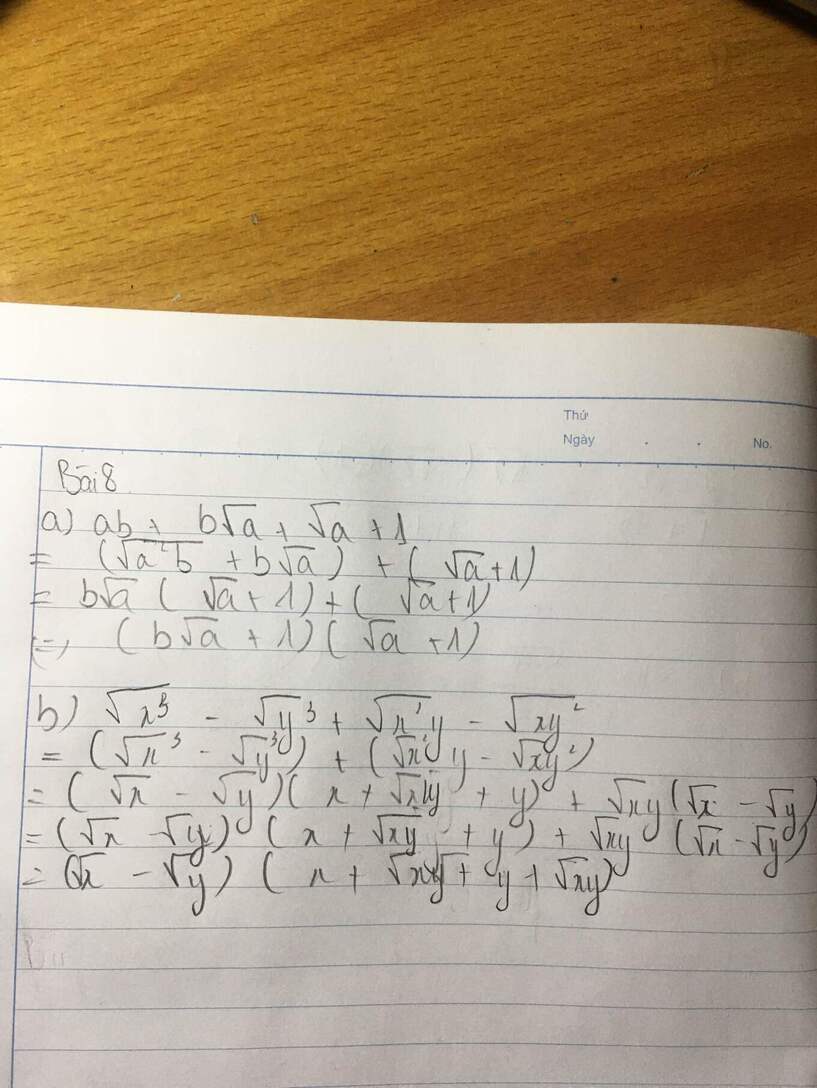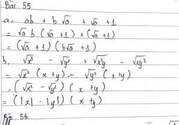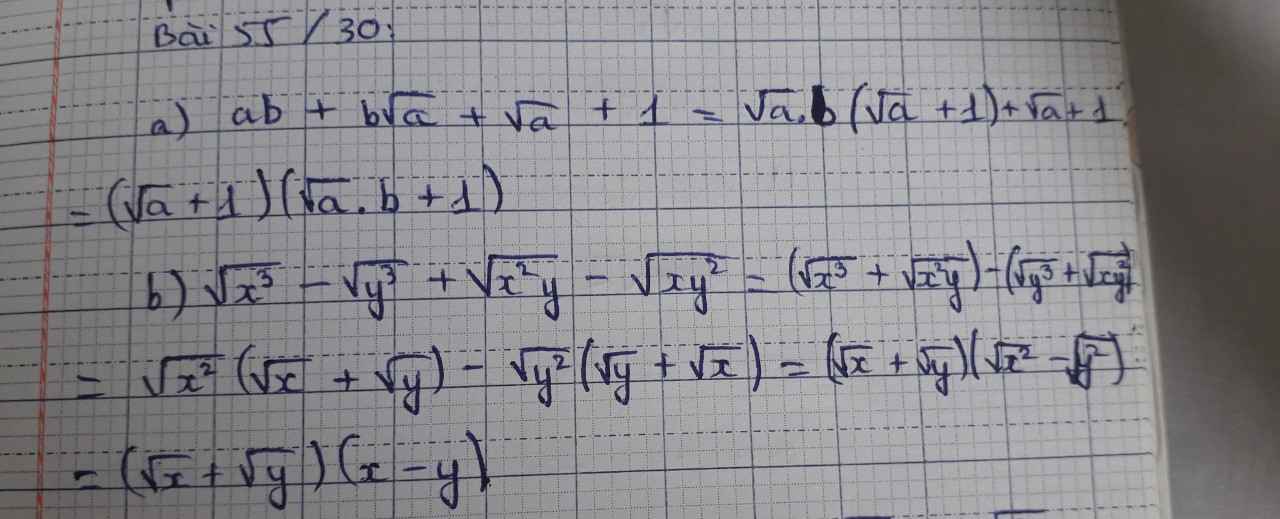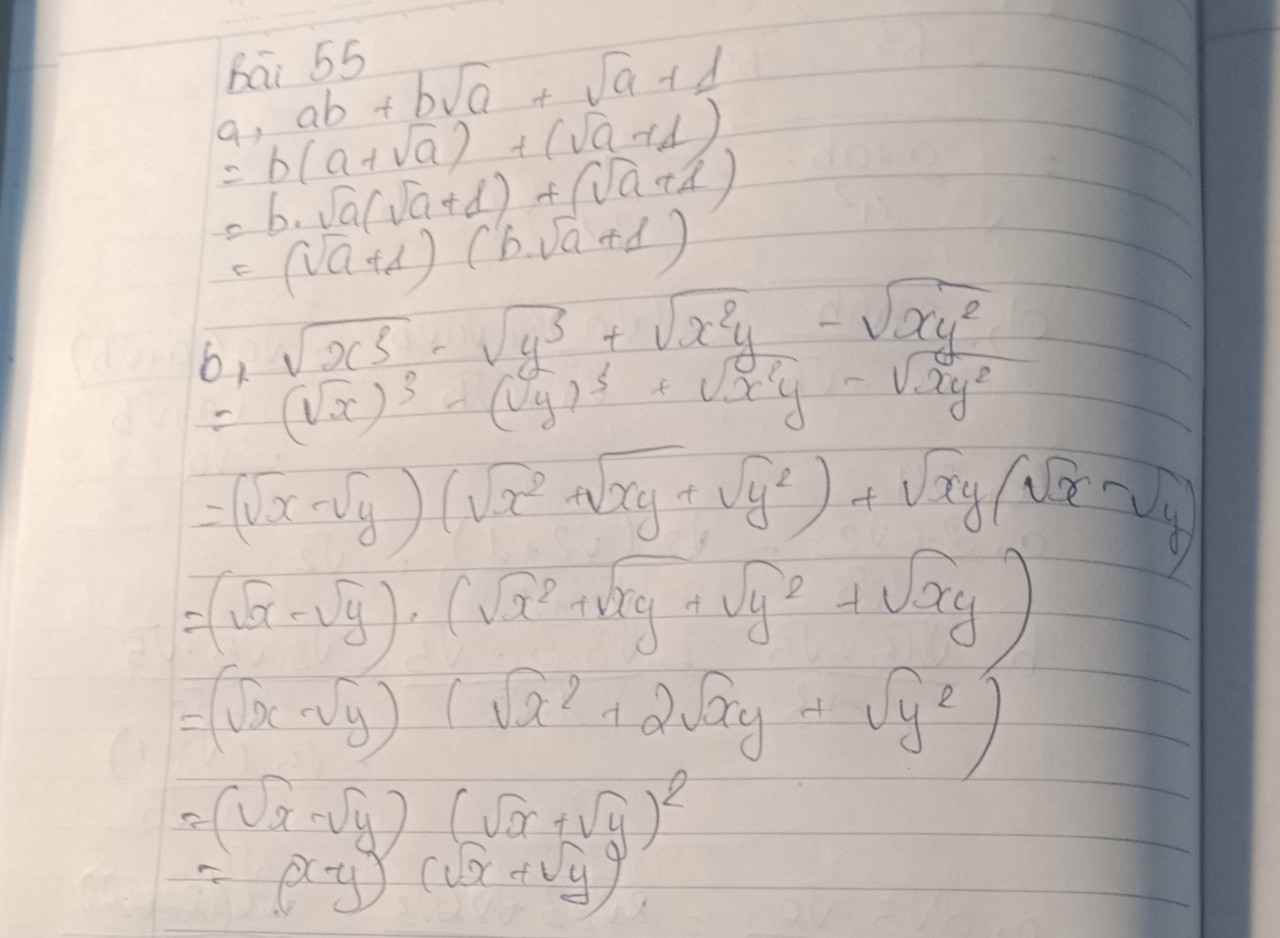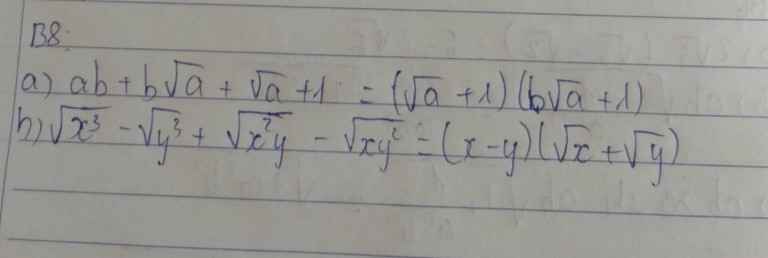Question

Bài 55 (trang 30 SGK Toán 9 Tập 1)

Phân tích thành nhân tử (với a, b, x, y là các số không âm)

a) $a b+b \sqrt{a}+\sqrt{a}+1$;

b) $\sqrt{x^{3}}-\sqrt{y^{3}}+\sqrt{x^{2} y}-\sqrt{x y^{2}}$.

Answer 1

a, \(ab+b\sqrt{a}+\sqrt{a}+1=\sqrt{a}b\left(\sqrt{a}+1\right)+\sqrt{a}+1\)

\(=\left(b\sqrt{a}+1\right)\left(\sqrt{a}+1\right)\)

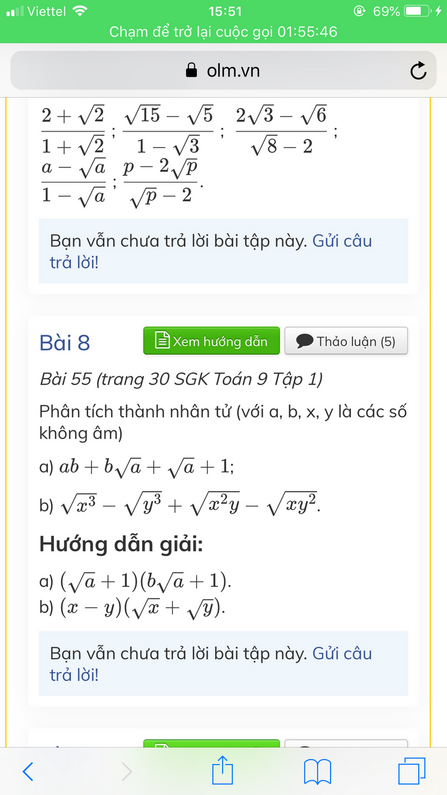
b, \(\sqrt{x^3}-\sqrt{y^3}+\sqrt{x^2y}-\sqrt{xy^2}\)

\(=\sqrt{x^2}\left(\sqrt{x}+\sqrt{y}\right)-\sqrt{y^2}\left(\sqrt{y}+\sqrt{x}\right)=\left(\left|x\right|-\left|y\right|\right)\left(\sqrt{x}+\sqrt{y}\right)\)

Answer 2

a) $(\sqrt{a}+1)(b\sqrt{a}+1)$.
b) $(x-y)(\sqrt{x}+\sqrt{y})$

Answer 3

a) \(ab+b\sqrt{a}+\sqrt{a}+1=b\sqrt{a}\left(\sqrt{a}+1\right)+\left(\sqrt{a}+1\right)=\left(b\sqrt{a}+1\right)\left(\sqrt{a}+1\right)\)

b) \(\sqrt{x^3}-\sqrt{y^3}+\sqrt{x^2y}-\sqrt{xy^2}=x\sqrt{x}-y\sqrt{y}+x\sqrt{y}-y\sqrt{x}=x\left(\sqrt{x}+\sqrt{y}\right)-y\left(\sqrt{x}+\sqrt{y}\right)=\left(x-y\right)\left(\sqrt{x}+\sqrt{y}\right)\)

Answer 4

a,\(ab+b\sqrt{a}+\sqrt{a}+1=b\sqrt{a}(\sqrt{a}+1)+ \sqrt{a}+1=(\sqrt{a}+1)(b\sqrt{a}+1)\)  

b,\(\sqrt{x^3}-\sqrt{y^3}+\sqrt{x^2y}-\sqrt{xy^2}=x\sqrt{x}-y\sqrt{y}+x\sqrt{y}-y\sqrt{x}=(x-y)(\sqrt{x}+\sqrt{y})\)

Answer 5

a)\(ab+b\sqrt{a}+\sqrt{a}+1\)

=\(\left(ab+b\sqrt{a}\right)+\left(\sqrt{a}+1\right)\)

=\([\left(\sqrt{a}\right)^2b+b\sqrt{a}]+\left(\sqrt{a}+1\right)\)

=\(\left(\sqrt{a}.\sqrt{a}.b+b\sqrt{a}\right)+\left(\sqrt{a}+1\right)\)

=\(b\sqrt{a}\left(\sqrt{a}+1\right)+\left(\sqrt{a}+1\right)\)

=\(\left(\sqrt{a}+1\right)\left(b\sqrt{a}+1\right)\)

b)

Answer 6

 

Answer 7

Answer 8

a) ab + b√a + √a + 1 = [(√a)2b + b√a] + (√a + 1)

= b√a(√a + 1) + (√a + 1) = (√a + 1)(b√a + 1)

= (√x - √y)(√x + √y)2

= (√x - √y)(√x + √y)(√x + √y)

= (x - y)(√x + √y)

Answer 9

a) $(\sqrt{a}+1)(b\sqrt{a}+1)$.
b) $(x-y)(\sqrt{x}+\sqrt{y})$.

Answer 10

Answer 11

a) (\sqrt{a}+1)(b \sqrt{a}+1)(a​+1)(ba​+1).
b) (x-y)(\sqrt{x}+\sqrt{y})(x−y)(x​+y​).

Answer 12

Answer 13

a\(\left(\sqrt{a}+1\right)\left(\sqrt{a}b+1\right)\)b\(\left(x-y\right)\left(\sqrt{x}+\sqrt{y}\right)\)

Answer 14

a) $(\sqrt{a}+1)(b\sqrt{a}+1)$.
b) $(x-y)(\sqrt{x}+\sqrt{y})$

Answer 15

a) ab + b√a + √a + 1 = [(√a)2b + b√a] + (√a + 1)

= b√a(√a + 1) + (√a + 1) = (√a + 1)(b√a + 1)

Answer 16

a,(\(\sqrt{a}\)+1)(\(b\sqrt{a}+1\))
b, (x-y)(\(\sqrt{x}+\sqrt{y}\))

Answer 17

a = (cana +1)(b can a +1 )

b =(x -y )(canx +can y)

Answer 18

 

Answer 19

 

Answer 20

Answer 21

a) (\sqrt{a}+1)(b \sqrt{a}+1)(a​+1)(ba​+1).
b) (x-y)(\sqrt{x}+\sqrt{y})(x−y)(x​+y​).

Answer 22

Answer 23

a, \(ab+b\sqrt{a}+\sqrt{a}+1=\sqrt{a}.\sqrt{a}.b+\sqrt{a}+b\sqrt{a}+1=\left(\sqrt{a}+1\right)\left(b\sqrt{a}+1\right)\)

b,\(\sqrt{x^3}-\sqrt{y^3}+\sqrt{x^2y}-\sqrt{xy^2}=x\sqrt{x}-y\sqrt{y}+x\sqrt{y}-y\sqrt{x}=\left(x-y\right)\left(\sqrt{x}+\sqrt{y}\right)\)

Answer 24

Answer 25

 

Answer 26

Answer 27

 

Answer 28

 

Answer 29

Answer 30