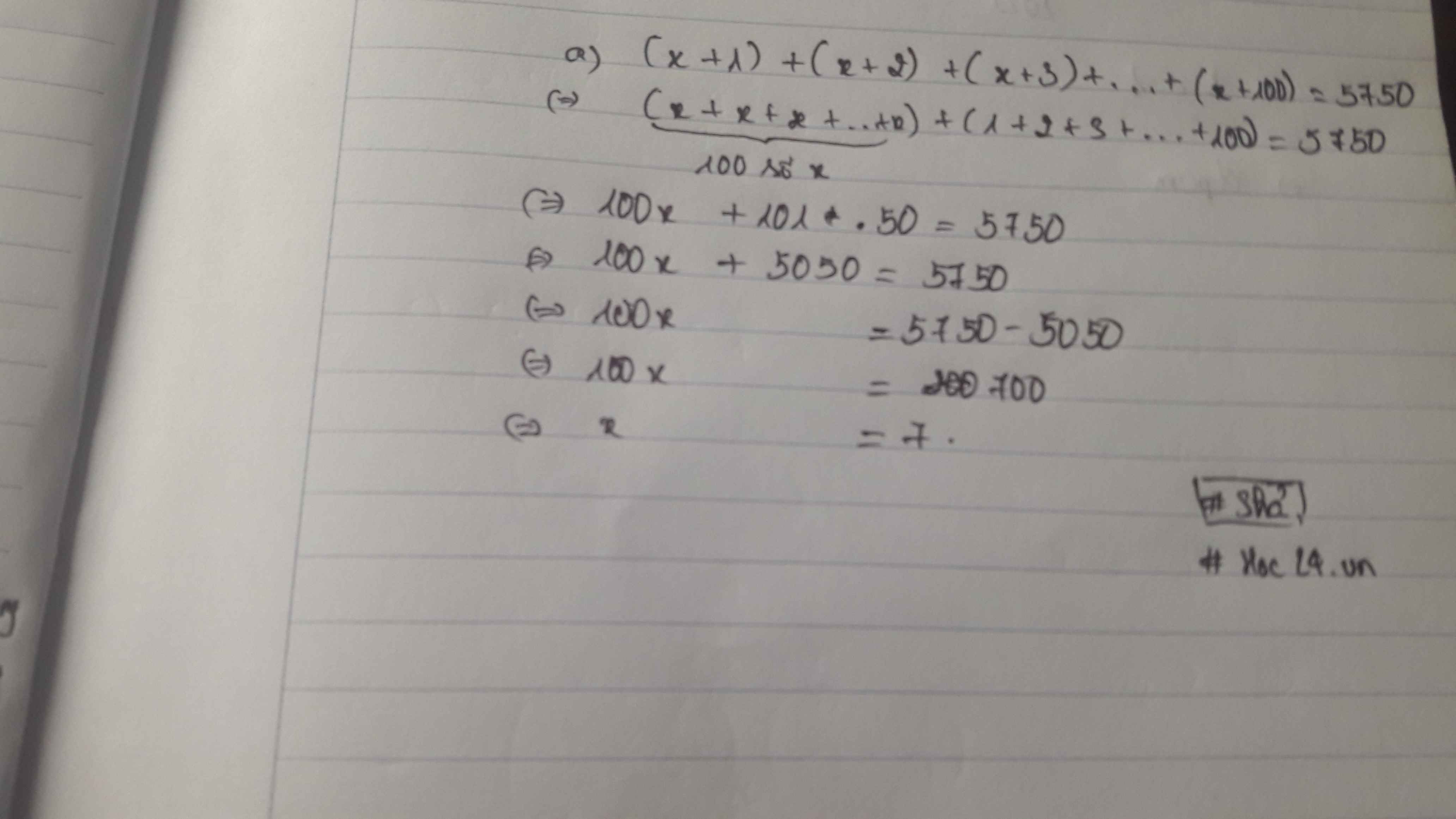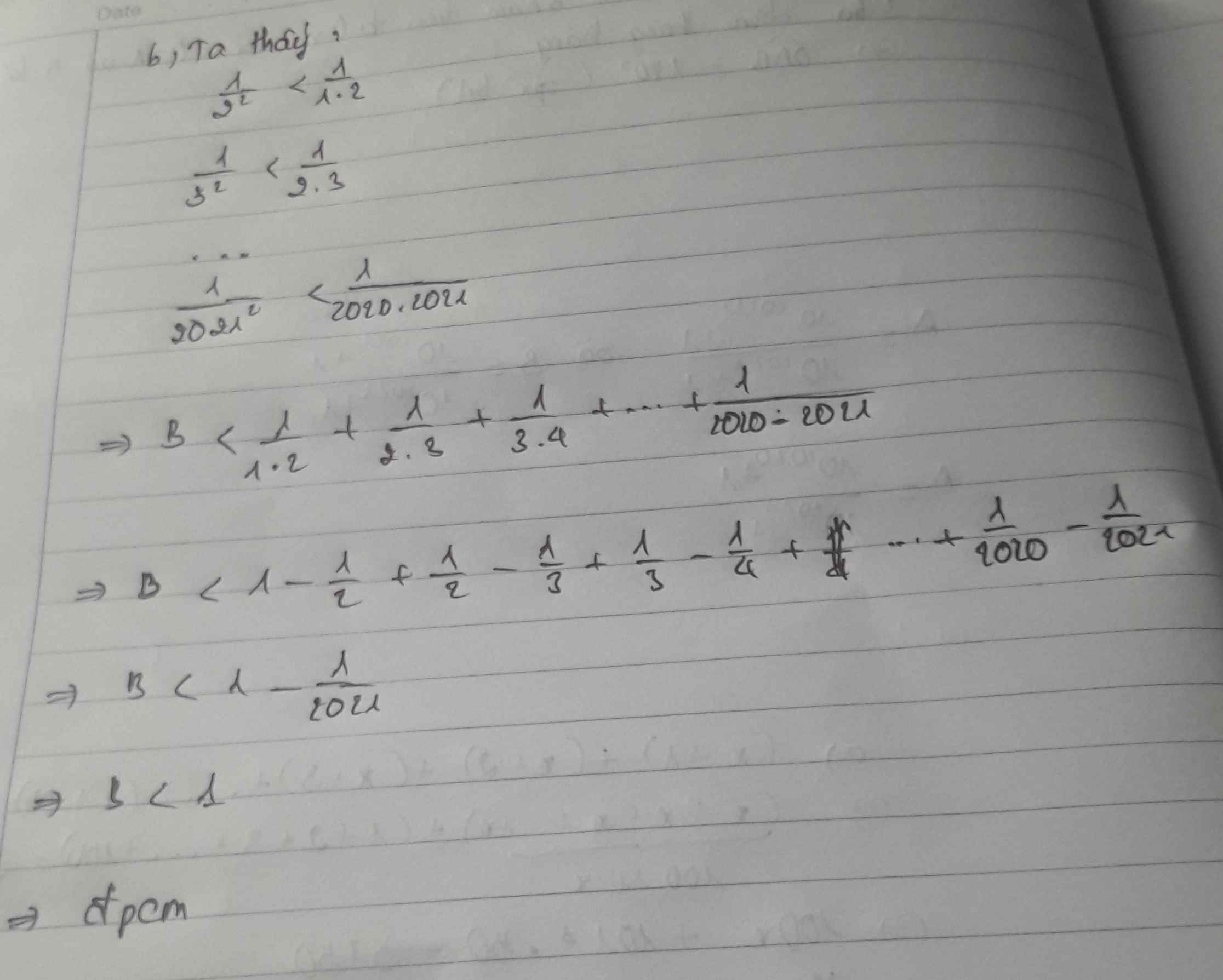\(∘backwin\)
\(a ) ( x + 1 ) + ( x + 2 ) + ( x + 3 ) + ... + ( x + 100 ) = 5750\)
\( ( x + x + x + ... + x ) + ( 1 + 2 + 3 + ... + 100 ) = 5750 \)
\( 100 x + ( 1 + 100 ) ×100 : 2 = 5750\)
\(100 x + 5050 = 5750\)
\( 100 x = 5750 − 5050\)
\(100 x = 700\)
\(x = 700 : 100\)
\(x = 7\)
\(b,\) \(B=\)\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{2021^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2020}+2021\)
\( B < 1 -\)\(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2020}-\dfrac{1}{2021}\)
\(B<1-\)\(\dfrac{1}{2021}\)
\(B<\)\(\dfrac{2020}{2021}\)
\(\dfrac{2020}{2021}< 1\)
\(B<1\)
a) (x+1) +(x+2 ) + ...+(x+100)=5750
= 100x + (1+2+3+...+100) = 5750
=100x + 5050 = 5750
--> 100x = 5750-5050=700
--> x=7
b) Ta thấy: 1/2^2 < 1/2.3
1/3^2 < 1/3.4
...
1/2021^2 < 1/2021.2022
--> B=1/2^2 + 1/3^2 + 1/4^2 + ...+ 1/2021^2 < 1/2.3 + 1/3.4 + ... +1/2021.2022 (1)
Ta có: 1/2.3 + 1/3.4 + ... +1/2021.2022
=1/2 - 1/3 + 1/3 - 1/4 + ... + 1/2021 - 1/2022
=1/2 - 1/2022 < 1 (2)
Từ (1) và (2) --> B<1 (đpcm)
<
\(a)\)
\(( x + 1 ) + ( x + 2 ) + ..... + ( x + 100 ) = 5750\)
\(\rightarrow \underbrace{x + x + ..... + x }_{ \text{100 lần x } }\) \(+ ( 1 + 2 + ..... + 100 ) = 5750\)
\(\rightarrow 100x + \dfrac{[( 100 - 1 ) : 1 + 1 ]( 100 + 1 )}{2} = 5750\)
\(\rightarrow 100x + 5050 = 5750\)
\(\rightarrow 100x = 700\)
\(\rightarrow x = 7\)
\(\text{ Vậy }\) \(x = 7 \)
\(b)\)
\(\text{ Ta có :}\)
\(\dfrac{1}{2^2} < \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2} < \dfrac{1}{2.3}\)
\(\dfrac{1}{4^2} < \dfrac{1}{3.4}\)
\(.......\)
\(\dfrac{1}{2021^2} < \dfrac{1}{2020.2021}\)
\(\rightarrow B = \dfrac{1}{2^2} + \dfrac{1}{3^2} + \dfrac{1}{4^2} + ......... + \dfrac{1}{2021^2} \) \(\rightarrow B < \dfrac{1}{1.2} + \dfrac{1}{2.3} + \dfrac{1}{3.4} + ........ \dfrac{1}{2020.2021}\)
\(\rightarrow B < 1 - \dfrac{1}{2} + \dfrac{1}{2} - \dfrac{1}{3} + ....... + \dfrac{1}{2020} - \dfrac{1}{2021}\)
\(\rightarrow B < 1 - \dfrac{1}{2021}\)
\(\rightarrow B < 1\)
\(\text{ Công thức tổng quát :}\)
\( \dfrac{1}{2^2} + ....... + \dfrac{1}{n^2} \) \(< \) \(\dfrac{1}{1.2} + \dfrac{1}{2.3} + ..... + \dfrac{1}{(n-1)n}\)