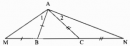
Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = \(\frac{1}{2}BM\); GC =\(\frac{2}{3}CN\) (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> \(\widehat{BAG}=\widehat{CAG}\) => G thuộc phân giác của \(\widehat{BAC}\)
Mà ∆ABI = ∆ACI (c.c.c)
=> \(\widehat{BAI}=\widehat{CAI}\) => I thuộc phân giác của \(\widehat{BAC}\)
Vì G, I cùng thuộc phân giác của \(\widehat{BAC}\) nên A, G, I thẳng hàng
- mik đag viết đề thì lỗi thông cảm ạ đại cơ