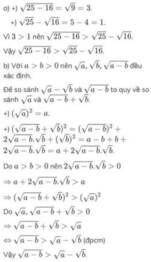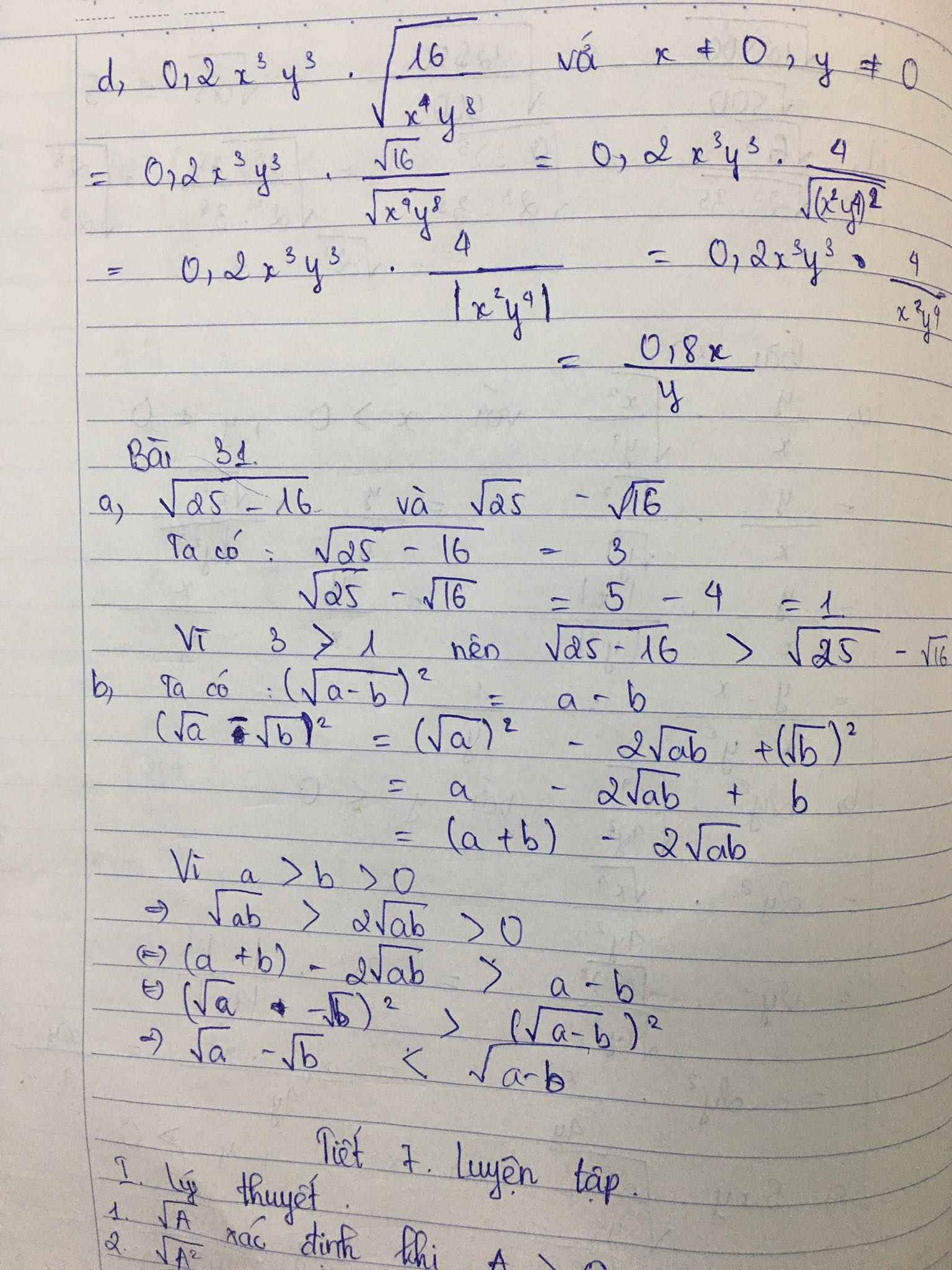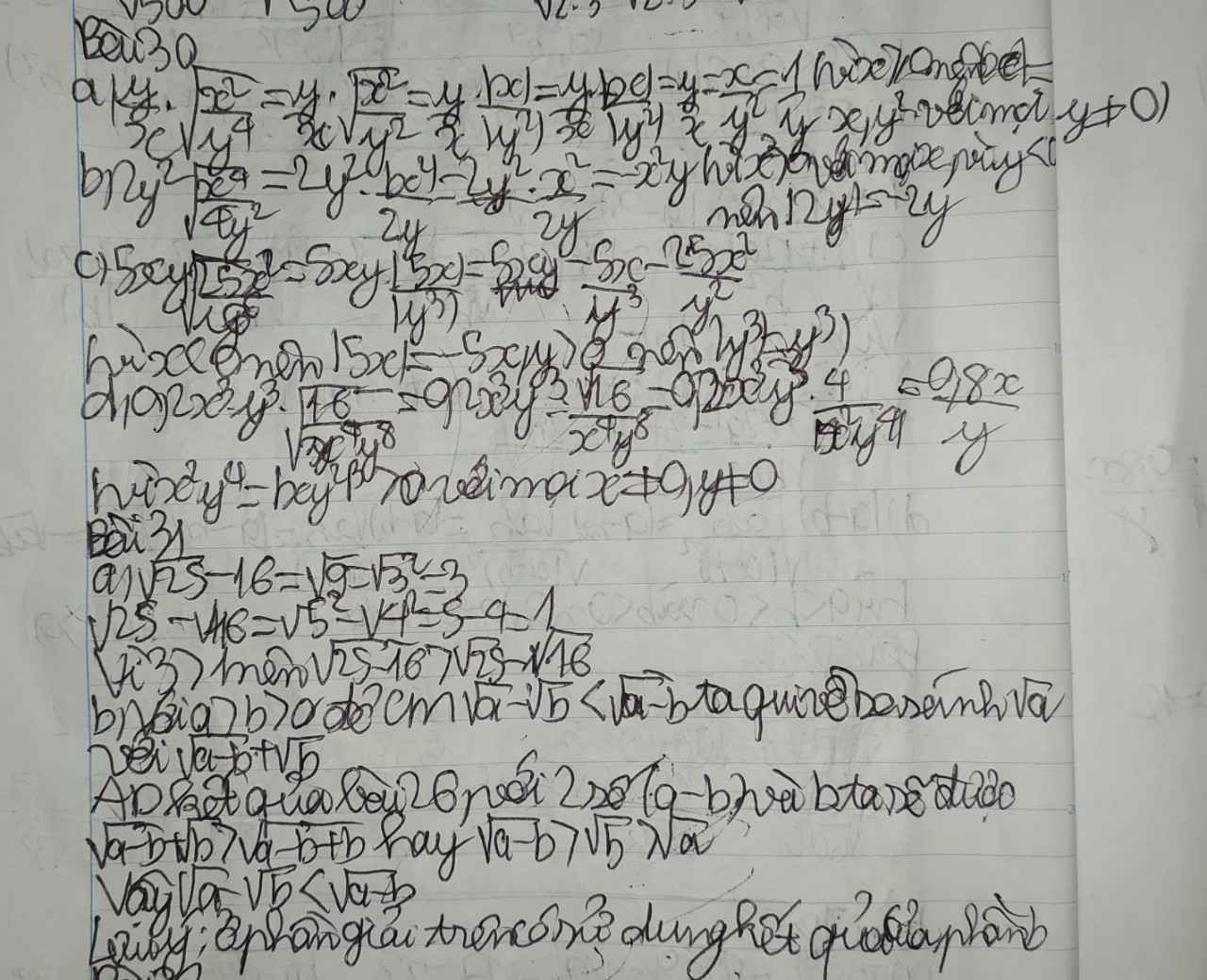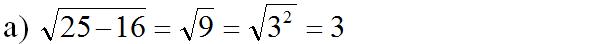Question

Bài 31 (trang 19 SGK Toán 9 Tập 1)

a) So sánh $\sqrt{25-16}$ và $\sqrt{25}-\sqrt{16}$ ;

b) Chứng minh rằng, với $a>b>0$ thì $\sqrt{a}-\sqrt{b}<\sqrt{a-b}$.

Answer 1

a, Ta có  \(\sqrt{25-16}=\sqrt{9}=3\)

\(\sqrt{25}-\sqrt{16}=5-4=1\)

Do 3 > 1 nên \(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)

Answer 2

a) căn 25 - 16  > căn 25 - căn 16

 

b)Với $a>b>0$ nên  \sqrt{a},\sqrt{b},\sqrt{a-b}a​,b​,− đều xác định

 

Để so sánh \sqrt{a}-\sqrt{b}a​−b​ và $-$ ta quy về so sánh \sqrt{a}a​ và \sqrt{a-b}+\sqrt{b}−+b​.

 

+) (\sqrt{a})^2=a(a​)2=a.

                                       

+) (\sqrt{a-b}+\sqrt{b})^2=(\sqrt{a-b})^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b})^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}(−+b​)2=(−)2+2−.b​+(b​)2=a−b+b+2−.b​=a+2−

.b​.

Do $a>b>0$ nên 2\sqrt{a-b}.\sqrt{b}>02−.b​>0

 

 

$\Rightarrow$ a+2\sqrt{a-b}.\sqrt{b}>aa+2−.b​>a

 

$\Rightarrow$ (\sqrt{a-b}+\sqrt{b})^2>(\sqrt{a})^2(−+b​)2>(a​)2

 

Do \sqrt{a},\sqrt{a-b}+\sqrt{b}>0a​,−+b​>0 

 

$\Rightarrow$ \sqrt{a-b}+\sqrt{b}>\sqrt{a}−+b​>a​

 

$\iff$ \sqrt{a-b}>\sqrt{a}-\sqrt{b}−>a​−b​ (đpcm)

 

Vậy \sqrt{a-b}>\sqrt{a}-\sqrt{b}−>a​−b​.

Answer 3

a) +) $\sqrt{25-16}=\sqrt{9}=3$.

    +) $\sqrt{25}-\sqrt{16}=5-4=1$.

Vì $3>1$ nên $\sqrt{25-16}>\sqrt{25}-\sqrt{16}$.

Vậy $\sqrt{25-16}>\sqrt{25}-\sqrt{16}$.

b) Với $a>b>0$ nên $\sqrt{a},\sqrt{b},\sqrt{a-b}$ đều xác định. 

Để so sánh $\sqrt{a}-\sqrt{b}$ và $\sqrt{a-b}$ ta quy về so sánh $\sqrt{a}$ và $\sqrt{a-b}+\sqrt{b}$.

+) $(\sqrt{a}{)}^2=a$.

+) $(\sqrt{a-b}+\sqrt{b}{)}^2=(\sqrt{a-b}{)}^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b}{)}^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}$.

Do $a>b>0$ nên $2\sqrt{a-b}.\sqrt{b}>0$

$\Rightarrow$ $a+2\sqrt{a-b}.\sqrt{b}>a$

$\Rightarrow$ $(\sqrt{a-b}+\sqrt{b}{)}^2>(\sqrt{a}{)}^2$

Do $\sqrt{a},\sqrt{a-b}+\sqrt{b}>0$ 

$\Rightarrow$ $\sqrt{a-b}+\sqrt{b}>\sqrt{a}$

$\iff$ $\sqrt{a-b}>\sqrt{a}-\sqrt{b}$ (đpcm)

Vậy $\sqrt{a-b}>\sqrt{a}-\sqrt{b}$.

Answer 4

a) +) $\sqrt{25-16}=\sqrt{9}=3$.

    +) $\sqrt{25}-\sqrt{16}=5-4=1$.

Vì $3>1$ nên $\sqrt{25-16}>\sqrt{25}-\sqrt{16}$.

Vậy $\sqrt{25-16}>\sqrt{25}-\sqrt{16}$.

b) Với $a>b>0$ nên $\sqrt{a},\sqrt{b},\sqrt{a-b}$ đều xác định. 

Để so sánh $\sqrt{a}-\sqrt{b}$ và $\sqrt{a-b}$ ta quy về so sánh $\sqrt{a}$ và $\sqrt{a-b}+\sqrt{b}$.

+) $(\sqrt{a}{)}^2=a$.

+) $(\sqrt{a-b}+\sqrt{b}{)}^2=(\sqrt{a-b}{)}^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b}{)}^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}$.

Do $a>b>0$ nên $2\sqrt{a-b}.\sqrt{b}>0$

$\Rightarrow$ $a+2\sqrt{a-b}.\sqrt{b}>a$

$\Rightarrow$ $(\sqrt{a-b}+\sqrt{b}{)}^2>(\sqrt{a}{)}^2$

Do $\sqrt{a},\sqrt{a-b}+\sqrt{b}>0$ 

$\Rightarrow$ $\sqrt{a-b}+\sqrt{b}>\sqrt{a}$

$\iff$ $\sqrt{a-b}>\sqrt{a}-\sqrt{b}$ (đpcm)

Vậy $\sqrt{a-b}>\sqrt{a}-\sqrt{b}$.

Answer 5

a) +) $\sqrt{25-16}=\sqrt{9}=3$.

    +) $\sqrt{25}-\sqrt{16}=5-4=1$.

Vì $3>1$ nên $\sqrt{25-16}>\sqrt{25}-\sqrt{16}$.

Vậy $\sqrt{25-16}>\sqrt{25}-\sqrt{16}$.

b) Với $a>b>0$ nên $\sqrt{a},\sqrt{b},\sqrt{a-b}$ đều xác định. 

Để so sánh $\sqrt{a}-\sqrt{b}$ và $\sqrt{a-b}$ ta quy về so sánh $\sqrt{a}$ và $\sqrt{a-b}+\sqrt{b}$.

+) $(\sqrt{a}{)}^2=a$.

+) $(\sqrt{a-b}+\sqrt{b}{)}^2=(\sqrt{a-b}{)}^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b}{)}^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}$.

Do $a>b>0$ nên $2\sqrt{a-b}.\sqrt{b}>0$

$\Rightarrow$ $a+2\sqrt{a-b}.\sqrt{b}>a$

$\Rightarrow$ $(\sqrt{a-b}+\sqrt{b}{)}^2>(\sqrt{a}{)}^2$

Do $\sqrt{a},\sqrt{a-b}+\sqrt{b}>0$ 

$\Rightarrow$ $\sqrt{a-b}+\sqrt{b}>\sqrt{a}$

$\iff$ $\sqrt{a-b}>\sqrt{a}-\sqrt{b}$ (đpcm)

Vậy $\sqrt{a-b}>\sqrt{a}-\sqrt{b}$

 

Answer 6

Answer 7

a) \(\sqrt{25-16}=\sqrt{9}=3;\sqrt{25}-\sqrt{16}=5-4=1;3>1\Rightarrow\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)

b) \(\left(\sqrt{a-b}+\sqrt{b}\right)^2=a-b+b+2\sqrt{a-b}\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}\)

    \(\)

Do $a>b>0$ nên 2\sqrt{a-b}.\sqrt{b}>02a−b​.b​>0

$\Rightarrow$ a+2\sqrt{a-b}.\sqrt{b}>aa+2a−b​.b​>a

$\Rightarrow$ (\sqrt{a-b}+\sqrt{b})^2>(\sqrt{a})^2(a−b​+b​)2>(a​)2

Do \sqrt{a},\sqrt{a-b}+\sqrt{b}>0a​,a−b​+b​>0 

$\Rightarrow$ \sqrt{a-b}+\sqrt{b}>\sqrt{a}a−b​+b​>a​

$\iff$ \sqrt{a-b}>\sqrt{a}-\sqrt{b}a−b​>a​−b​ (đpcm)

Vậy \sqrt{a-b}>\sqrt{a}-\sqrt{b}a−b​>a​−b​.

Answer 8

a) +) \sqrt{25-16}=\sqrt{9}=325−16​=9​=3.

    +) \sqrt{25}-\sqrt{16} = 5-4 = 125​−16​=5−4=1.

Vì $3>1$ nên \sqrt{25-16}>\sqrt{25}-\sqrt{16}25−16​>25​−16​.

Vậy \sqrt{25-16}>\sqrt{25}-\sqrt{16}25−16​>25​−16​.

b) Với $a>b>0$ nên \sqrt{a},\sqrt{b},\sqrt{a-b}a​,b​,a−b​ đều xác định. 

Để so sánh \sqrt{a}-\sqrt{b}a​−b​ và \sqrt{a-b}a−b​ ta quy về so sánh \sqrt{a}a​ và \sqrt{a-b}+\sqrt{b}a−b​+b​.

+) (\sqrt{a})^2=a(a​)2=a.

+) (\sqrt{a-b}+\sqrt{b})^2=(\sqrt{a-b})^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b})^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}(a−b​+b​)2=(a−b​)2+2a−b​.b​+(b​)2=a−b+b+2a−b​.b​=a+2a−b​.b​.

Do $a>b>0$ nên 2\sqrt{a-b}.\sqrt{b}>02a−b​.b​>0

$\Rightarrow$ a+2\sqrt{a-b}.\sqrt{b}>aa+2a−b​.b​>a

$\Rightarrow$ (\sqrt{a-b}+\sqrt{b})^2>(\sqrt{a})^2(a−b​+b​)2>(a​)2

Do \sqrt{a},\sqrt{a-b}+\sqrt{b}>0a​,a−b​+b​>0 

$\Rightarrow$ \sqrt{a-b}+\sqrt{b}>\sqrt{a}a−b​+b​>a​

$\iff$ \sqrt{a-b}>\sqrt{a}-\sqrt{b}a−b​>a​−b​ (đpcm)

Vậy \sqrt{a-b}>\sqrt{a}-\sqrt{b}a−b​>a​−b​.

Answer 9

a) +) $\sqrt{25-16}=\sqrt{9}=3$.

    +) $\sqrt{25}-\sqrt{16}=5-4=1$.

Vì $3>1$ nên $\sqrt{25-16}>\sqrt{25}-\sqrt{16}$.

Vậy $\sqrt{25-16}>\sqrt{25}-\sqrt{16}$.

b) Với $a>b>0$ nên $\sqrt{a},\sqrt{b},\sqrt{a-b}$ đều xác định. 

Để so sánh $\sqrt{a}-\sqrt{b}$ và $\sqrt{a-b}$ ta quy về so sánh $\sqrt{a}$ và $\sqrt{a-b}+\sqrt{b}$.

+) $(\sqrt{a}{)}^2=a$.

+) $(\sqrt{a-b}+\sqrt{b}{)}^2=(\sqrt{a-b}{)}^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b}{)}^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}$.

Do $a>b>0$ nên $2\sqrt{a-b}.\sqrt{b}>0$

$\Rightarrow$ $a+2\sqrt{a-b}.\sqrt{b}>a$

$\Rightarrow$ $(\sqrt{a-b}+\sqrt{b}{)}^2>(\sqrt{a}{)}^2$

Do $\sqrt{a},\sqrt{a-b}+\sqrt{b}>0$ 

$\Rightarrow$ $\sqrt{a-b}+\sqrt{b}>\sqrt{a}$

$\iff$ $\sqrt{a-b}>\sqrt{a}-\sqrt{b}$ (đpcm)

Vậy $\sqrt{a-b}>\sqrt{a}-\sqrt{b}$.
 

Answer 10

a) +) $\sqrt{25-16}=\sqrt{9}=3$.

    +) $\sqrt{25}-\sqrt{16}=5-4=1$.

Vì $3>1$ nên $\sqrt{25-16}>\sqrt{25}-\sqrt{16}$.

Vậy $\sqrt{25-16}>\sqrt{25}-\sqrt{16}$.

b) Với $a>b>0$ nên $\sqrt{a},\sqrt{b},\sqrt{a-b}$ đều xác định. 

Để so sánh $\sqrt{a}-\sqrt{b}$ và $\sqrt{a-b}$ ta quy về so sánh $\sqrt{a}$ và $\sqrt{a-b}+\sqrt{b}$.

+) $(\sqrt{a}{)}^2=a$.

+) $(\sqrt{a-b}+\sqrt{b}{)}^2=(\sqrt{a-b}{)}^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b}{)}^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}$.

Do $a>b>0$ nên $2\sqrt{a-b}.\sqrt{b}>0$

$\Rightarrow$ $a+2\sqrt{a-b}.\sqrt{b}>a$

$\Rightarrow$ $(\sqrt{a-b}+\sqrt{b}{)}^2>(\sqrt{a}{)}^2$

Do $\sqrt{a},\sqrt{a-b}+\sqrt{b}>0$ 

$\Rightarrow$ $\sqrt{a-b}+\sqrt{b}>\sqrt{a}$

$\iff$ $\sqrt{a-b}>\sqrt{a}-\sqrt{b}$ (đpcm)

Vậy $\sqrt{a-b}>\sqrt{a}-\sqrt{b}$.
 

Answer 11

a) +) \sqrt{25-16}=\sqrt{9}=325−16​=9​=3.

    +) \sqrt{25}-\sqrt{16} = 5-4 = 125​−16​=5−4=1.

Vì $3>1$ nên \sqrt{25-16}>\sqrt{25}-\sqrt{16}25−16​>25​−16​.

Vậy \sqrt{25-16}>\sqrt{25}-\sqrt{16}25−16​>25​−16​.

b) Với $a>b>0$ nên \sqrt{a},\sqrt{b},\sqrt{a-b}a​,b​,a−b​ đều xác định. 

Để so sánh \sqrt{a}-\sqrt{b}a​−b​ và \sqrt{a-b}a−b​ ta quy về so sánh \sqrt{a}a​ và \sqrt{a-b}+\sqrt{b}a−b​+b​.

+) (\sqrt{a})^2=a(a​)2=a.

+) (\sqrt{a-b}+\sqrt{b})^2=(\sqrt{a-b})^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b})^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}(a−b​+b​)2=(a−b​)2+2a−b​.b​+(b​)2=a−b+b+2a−b​.b​=a+2a−b​.b​.

Do $a>b>0$ nên 2\sqrt{a-b}.\sqrt{b}>02a−b​.b​>0

$\Rightarrow$ a+2\sqrt{a-b}.\sqrt{b}>aa+2a−b​.b​>a

$\Rightarrow$ (\sqrt{a-b}+\sqrt{b})^2>(\sqrt{a})^2(a−b​+b​)2>(a​)2

Do \sqrt{a},\sqrt{a-b}+\sqrt{b}>0a​,a−b​+b​>0 

$\Rightarrow$ \sqrt{a-b}+\sqrt{b}>\sqrt{a}a−b​+b​>a​

$\iff$ \sqrt{a-b}>\sqrt{a}-\sqrt{b}a−b​>a​−b​ (đpcm)

Vậy \sqrt{a-b}>\sqrt{a}-\sqrt{b}a−b​>a​−b​.

Answer 12

a, Ta có \(\sqrt{25-16}=\sqrt{9}=3\)
               \(\sqrt{25}-\sqrt{16}=5-4=1\)
Vì 3>1 nên \(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)

b, Quy về so sánh \(\sqrt{a}\) với \(\sqrt{a-b}+\sqrt{b}\)
Với 2 số (a-b) và b
\(\sqrt{a-b}+\sqrt{b}>\sqrt{a-b+b}\)
<=> \(\sqrt{a-b}+\sqrt{b}>\sqrt{a}\) 
<=>\(\sqrt{a-b}>\sqrt{a}-\sqrt{b}\)
<=>\(\sqrt{a}-\sqrt{b}< \sqrt{a-b}\) (đpcm)

 

Answer 13

a,\(\sqrt{25-16}=\sqrt{9}=\sqrt{3^2}=3\)

\(\sqrt{25}-\sqrt{16}=\sqrt{5^2}-\sqrt{4^2}=5-4=1\)

ví 3>1 nên :

\(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)

b,Với a>b> thì \(\sqrt{a}-\sqrt{b}< \sqrt{a-b}\)

ta qui về so sánh\(\sqrt{a}\) với\(\sqrt{a-b}+\sqrt{b}\)

Aps dụng về kết quả bài 26 , với 2 số (a-b) và b ta sẽ được :

\(\sqrt{a-b}+\sqrt{b}>\sqrt{a-b+b}hay^{ }\sqrt{a-b}+\sqrt{b}>\sqrt{a}\)

 

Answer 14

a ,\(\sqrt{25-16}\) =\(\sqrt{9}\) =3

\(\sqrt{25}\) -\(\sqrt{16}\) = 5 - 4 = 1

vì 3>1 nên \(\sqrt{25-16}\) > \(\sqrt{25}\)- \(\sqrt{16}\) 

b, a>b>c thì \(\sqrt{a}\) - \(\sqrt{b}\) <\(\sqrt{a-b}\)

so sánh \(\sqrt{a}\) với \(\sqrt{a-b}\)+\(\sqrt{b}\) :  áp dụng kết quả bài 26 : \(\sqrt{a+b}\) <\(\sqrt{a}\)+\(\sqrt{b}\) 

với 2 số :(a-b) và b : \(\sqrt{a-b}\) +\(\sqrt{b}\)> \(\sqrt{a-b+b}\)

                                \(\sqrt{a-b}+\sqrt{b>\sqrt{a}}\)

                                 \(\sqrt{a-b}>\sqrt{a}-\sqrt{b}\) (đpcm)

 

Answer 15

a) +) √25−16=√9=3.

    +) √25−√16=5−4=1.

Vì 3>1 nên √25−16>√25−√16.

Vậy √25−16>√25−√16.

b) Với a>b>0 nên √a,√b,√a−b đều xác định. 

Để so sánh √a−√b và √a−b ta quy về so sánh √a và √a−b+√b.

2=a.

222=a−b+b+2√a−b.√b=a+2√a−b.√b.

Do a>b>0 nên 2√a−b.√b>0

⇒ a+2√a−b.√b>a

22

Do √a,√a−b+√b>0 

⇒ √a−b+√b>√a

⇔ √a−b>√a−√b (đpcm)

Vậy √a−b>√a−√b.

Answer 16

Answer 17

Answer 18

a,\(\sqrt{25-16}=\sqrt{9}=3\)

\(\sqrt{25}-\sqrt{16}=5-4=1\)

vì \(3>1\) nên \(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)

vậy \(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)

b) Với $a>b>0$ nên\(\sqrt{a,}\sqrt{b,}\sqrt{a-b}\) đều xác định

để so sánh \(\sqrt{a}-\sqrt{b}\) và \(\sqrt{a-b}\) ta quy về so sánh \(\sqrt{a}\) và\(\sqrt{a-b}+\sqrt{b}\)

 

) (\sqrt{a})^2=a(a​)2=a.

+) (\sqrt{a-b}+\sqrt{b})^2=(\sqrt{a-b})^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b})^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}(a−b​+b​)2=(a−b​)2+2a−b​.b​+(b​)2=a−b+b+2a−b​.b​=a+2a−b​.b​.

Do $a>b>0$ nên 2\sqrt{a-b}.\sqrt{b}>02a−b​.b​>0

$\Rightarrow$ a+2\sqrt{a-b}.\sqrt{b}>aa+2a−b​.b​>a

$\Rightarrow$ (\sqrt{a-b}+\sqrt{b})^2>(\sqrt{a})^2(a−b​+b​)2>(a​)2

Do \sqrt{a},\sqrt{a-b}+\sqrt{b}>0a​,a−b​+b​>0 

$\Rightarrow$ \sqrt{a-b}+\sqrt{b}>\sqrt{a}a−b​+b​>a​

$\iff$ \sqrt{a-b}>\sqrt{a}-\sqrt{b}a−b​>a​−b​ (đpcm)

Vậy \sqrt{a-b}>\sqrt{a}-\sqrt{b}a−b​>a​−b​.

 

 

 

 

Answer 19

Answer 20

a) Vì 3 > 1 nên căn 25-16 > căn 25 - căn 16

Vậy căn 25-16 > căn 25- căn 16

Answer 21

Answer 22

.

Answer 23

a) +) √25−16=√9=3.

    +) √25−√16=5−4=1.

Vì 3>1 nên √25−16>√25−√16.

Vậy √25−16>√25−√16.

b) Với a>b>0 nên √a,√b,√a−b đều xác định. 

Để so sánh √a−√b và √a−b ta quy về so sánh √a và √a−b+√b.

2=a.

222=a−b+b+2√a−b.√b=a+2√a−b.√b.

Do a>b>0 nên 2√a−b.√b>0

⇒ a+2√a−b.√b>a

22

Do √a,√a−b+√b>0 

⇒ √a−b+√b>√a

⇔ √a−b>√a−√b (đpcm)

Vậy √a−b>√a−√b.

Answer 24

a,\(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)

b,

Answer 25

a) +) \sqrt{25-16}=\sqrt{9}=325−16​=9​=3.

    +) \sqrt{25}-\sqrt{16} = 5-4 = 125​−16​=5−4=1.

Vì $3>1$ nên \sqrt{25-16}>\sqrt{25}-\sqrt{16}25−16​>25​−16​.

Vậy \sqrt{25-16}>\sqrt{25}-\sqrt{16}25−16​>25​−16​.

b) Với $a>b>0$ nên \sqrt{a},\sqrt{b},\sqrt{a-b}a​,b​,a−b​ đều xác định. 

Để so sánh \sqrt{a}-\sqrt{b}a​−b​ và \sqrt{a-b}a−b​ ta quy về so sánh \sqrt{a}a​ và \sqrt{a-b}+\sqrt{b}a−b​+b​.

+) (\sqrt{a})^2=a(a​)2=a.

+) (\sqrt{a-b}+\sqrt{b})^2=(\sqrt{a-b})^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b})^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}(a−b​+b​)2=(a−b​)2+2a−b​.b​+(b​)2=a−b+b+2a−b​.b​=a+2a−b​.b​.

Do $a>b>0$ nên 2\sqrt{a-b}.\sqrt{b}>02a−b​.b​>0

$\Rightarrow$ a+2\sqrt{a-b}.\sqrt{b}>aa+2a−b​.b​>a

$\Rightarrow$ (\sqrt{a-b}+\sqrt{b})^2>(\sqrt{a})^2(a−b​+b​)2>(a​)2

Do \sqrt{a},\sqrt{a-b}+\sqrt{b}>0a​,a−b​+b​>0 

$\Rightarrow$ \sqrt{a-b}+\sqrt{b}>\sqrt{a}a−b​+b​>a​

$\iff$ \sqrt{a-b}>\sqrt{a}-\sqrt{b}a−b​>a​−b​ (đpcm)

Vậy \sqrt{a-b}>\sqrt{a}-\sqrt{b}a−b​>a​−b​.

Answer 26

 

√25 - √16 = √52 - √42 = 5 - 4 = 1

Vì 3 > 1 nên 

Answer 27

a) \(\sqrt{25-16}\) = \(\sqrt{9}\) = 3

     \(\sqrt{25}\) - \(\sqrt{16}\) = 5 - 4 = 1

Vì 3 > 1 nên \(\sqrt{25-16}\) > \(\sqrt{25}\) - \(\sqrt{16}\)

b) Vì a > b > 0 nên a-b > 0

Theo kết quả ở bài 26 với a>0 , b> 0 thì :

\(\sqrt{a+b}< \sqrt{a}+\sqrt{b}\)

Áp dụng kết quả bài 26 với 2 số a-b > 0 và  b> 0  ta được :

     \(\sqrt{\left(a-b\right)+b}< \sqrt{a-b}+\sqrt{b}\)                    

⇔ \(\sqrt{a}< \sqrt{a-b}+\sqrt{b}\)

⇔ \(\sqrt{a}-\sqrt{b}< \sqrt{a-b}\) ( đpcm

 

Answer 28

a)\(\sqrt{25-16}=\sqrt{9}=3\)                 \(\sqrt{25}-\sqrt{16}=5-4=1\) Vì3>1 nên \(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\) vậy \(\sqrt{25-16}>\sqrt{25}-\sqrt{16}\)        b)vớia>b>0 nên \(\sqrt{a},\sqrt{b},\sqrt{a-b}\) đều xác định do a>b>0 nên \(2\sqrt{a-b}.\sqrt{b}>0\) \(\Rightarrow a+2\sqrt{a-b.\sqrt{b}>a}\) vậy \(\sqrt{a-b}>\sqrt{a}—\sqrt{b}\)

Answer 29

a.\(\sqrt{25-16}\) Lớn hơn \(\sqrt{25}-\sqrt{16}\)

b.ta có \(\sqrt{a}-\sqrt{b}\) nhỏ hơn \(\sqrt{a-b}\)                                                                                                          \(\Leftrightarrow\sqrt{a}nhỏ\sqrt{a-b}+\sqrt{b}\Leftrightarrow(\sqrt{a}^2)nhỏ(\sqrt{a-b}-\sqrt{b^2})\)                                                                        \(\Leftrightarrow a\) nhỎ a - b \(+2\sqrt{b(a-b)}+b\Leftrightarrow2\sqrt{b(a-b)}\) lớn hơn 0                                                                    vậy \(\sqrt{a}-\sqrt{b}\) nhỏ \(\sqrt{a-b}\)

Answer 30

a) +) \sqrt{25-16}=\sqrt{9}=325−16​=9​=3.

    +) \sqrt{25}-\sqrt{16} = 5-4 = 125​−16​=5−4=1.

Vì $3>1$ nên \sqrt{25-16}>\sqrt{25}-\sqrt{16}25−16​>25​−16​.

Vậy \sqrt{25-16}>\sqrt{25}-\sqrt{16}25−16​>25​−16​.

b) Với $a>b>0$ nên \sqrt{a},\sqrt{b},\sqrt{a-b}a​,b​,a−b​ đều xác định. 

Để so sánh \sqrt{a}-\sqrt{b}a​−b​ và \sqrt{a-b}a−b​ ta quy về so sánh \sqrt{a}a​ và \sqrt{a-b}+\sqrt{b}a−b​+b​.

+) (\sqrt{a})^2=a(a​)2=a.

+) (\sqrt{a-b}+\sqrt{b})^2=(\sqrt{a-b})^2+2\sqrt{a-b}.\sqrt{b}+(\sqrt{b})^2=a-b+b+2\sqrt{a-b}.\sqrt{b}=a+2\sqrt{a-b}.\sqrt{b}(a−b​+b​)2=(a−b​)2+2a−b​.b​+(b​)2=a−b+b+2a−b​.b​=a+2a−b​.b​.

Do $a>b>0$ nên 2\sqrt{a-b}.\sqrt{b}>02a−b​.b​>0

$\Rightarrow$ a+2\sqrt{a-b}.\sqrt{b}>aa+2a−b​.b​>a

$\Rightarrow$ (\sqrt{a-b}+\sqrt{b})^2>(\sqrt{a})^2(a−b​+b​)2>(a​)2

Do \sqrt{a},\sqrt{a-b}+\sqrt{b}>0a​,a−b​+b​>0 

$\Rightarrow$ \sqrt{a-b}+\sqrt{b}>\sqrt{a}a−b​+b​>a​

$\iff$ \sqrt{a-b}>\sqrt{a}-\sqrt{b}a−b​>a​−b​ (đpcm)

Vậy \sqrt{a-b}>\sqrt{a}-\sqrt{b}a−b​>a​−b​.